题目内容
5.已知函数f(x)=$\frac{1}{2}{x^2}$+alnx,若对任意两个不等的正实数x1,x2都有$\frac{{f(x{\;}_1)-f({x_2})}}{{{x_1}-{x_2}}}$>2恒成立,则实数a的取值范围是[1,+∞).分析 方法一:由题意可知:当x>0时,f′(x)>2恒成立,则a>2x-2x2,在(0,+∞)上恒成立,即a>g(x)max,根据二次函数的性质,即可求得实数a的取值范围;
方法二:构造函数g(x)=f(x)-2x,x>0,求导,由题意可知f′(x)>2,(0,+∞)上恒成立,则a>h(x)max,根据二次函数的性质,即可求得实数a的取值范围.
解答 解:方法一:对任意两个不等的正实数x1,x2都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>2恒成立,
则当x>0时,f′(x)>2恒成立
f′(x)=x+$\frac{a}{x}$>2,在(0,+∞)上恒成立,
则a>2x-x2,在(0,+∞)上恒成立,
设g(x)=2x-x2,x>0,
函数的对称轴为x=1,
则当x=1时,取最大值,最大值为g(x)max=1,
∴a>1,
则实数a的取值范围[1,+∞),
故答案为:[1,+∞).
方法二:设g(x)=f(x)-2x,x>0,
求导g′(x)=f′(x)-2,
由$\frac{{f(x{\;}_1)-f({x_2})}}{{{x_1}-{x_2}}}$>2,则g′(x)=f′(x)-2>0,
则f′(x)>2,即f′(x)=x+$\frac{a}{x}$≥2,在(0,+∞)上恒成立,
则a≥2x-x2,在(0,+∞)上恒成立,
设h(x)=2x-x2,x>0,
函数的对称轴为x=1,
则当x=1时,取最大值,最大值为h(x)max=1,
∴a≥1,
则实数a的取值范围[1,+∞),
故答案为:[1,+∞).
点评 本题考查导数的意义,利用求函数的最值,考查二次函数的性质,考查计算能力,属于中档题.

练习册系列答案
相关题目
13.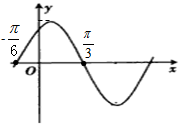 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象向左平移$\frac{π}{12}$单位得到的部分图象如图,则φ=( )| A. | $\frac{π}{6}$ | B. | -$\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{2}$ |
20.如图,某组合体的三视图是由边长为2的正方形和直径为2的圆组成,则它的体积为( )


| A. | 4+4π | B. | 8+4π | C. | $4+\frac{4}{3}π$ | D. | $8+\frac{4}{3}π$ |
10.若θ是直线l的倾斜角,且sinθ+cosθ=$\frac{{\sqrt{5}}}{5}$,则l的斜率为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{2}$或-2 | C. | $\frac{1}{2}$或2 | D. | -2 |
17.直线y=a与y=2x-3及曲线y=x+ex分别交于A、B两点,则|AB|的最小值为( )
| A. | $\frac{3}{2}$ | B. | e | C. | 3 | D. | 2 |
13.已知一空间几何体的三视图如图所示,其中俯视图为正方形,则该几何体的外接球的表面积为( )


| A. | 27π | B. | 49π | C. | 81π | D. | 100π |