题目内容
已知函数 处取得极值2
处取得极值2
(1)求函数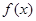 的表达式;
的表达式;
(2)当 满足什么条件时,函数
满足什么条件时,函数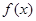 在区间
在区间 上单调递增?
上单调递增?
(3)若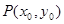 为
为 图象上任意一点,直线与
图象上任意一点,直线与 的图象相切于点P,求直线的斜率
的图象相切于点P,求直线的斜率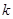 的取值范围
的取值范围
(1)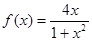 ;(2)当
;(2)当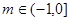 时,函数
时,函数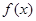 在区间
在区间 上单调递增;(3)直线的斜率
上单调递增;(3)直线的斜率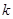 的取值范围是
的取值范围是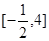
解析试题分析:(1) 求导得
求导得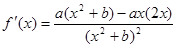 ,因为函数
,因为函数 在
在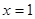 处取得极值2,
处取得极值2,
所以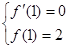 ,由此解得
,由此解得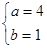 ,从而得
,从而得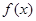 的解析式;(2)由(1)知
的解析式;(2)由(1)知 ,由此可得
,由此可得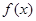 的单调增区间是[-1,1],要使得函数
的单调增区间是[-1,1],要使得函数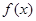 在区间
在区间 上单调递增,则
上单调递增,则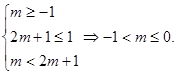 (3)由题意及导数的几何意义知,求直线的斜率
(3)由题意及导数的几何意义知,求直线的斜率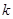 的取值范围就是求函数
的取值范围就是求函数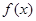 的导数的取值范围
的导数的取值范围
试题解析:(1) 因为
因为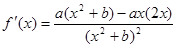 (2分)
(2分)
而函数 在
在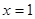 处取得极值2,
处取得极值2,
所以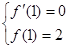 , 即
, 即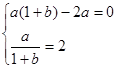 解得
解得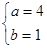
所以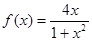 即为所求 (4分)
即为所求 (4分)
(2)由(1)知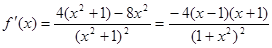
令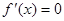 得:
得:
则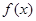 的增减性如下表:
的增减性如下表:
可知,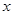
(-∞,-1) (-1,1) (1,+∞) 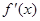
负 正 负 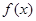
递减 递增 递减 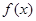 的单调增区间是[-1,1], (6分)
的单调增区间是[-1,1], (6分)
所以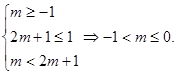
所以当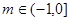 时,函数
时,函数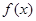 在区间
在区间 上单调递增。 (9分)
上单调递增。 (9分)
(3)由条件知,过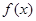 的图象上一点P的切线的斜率
的图象上一点P的切线的斜率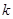 为:
为: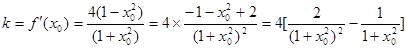 (11分)
(11分)
令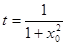 ,则
,则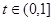 ,
,
此时,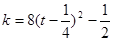 的图象性质知:
的图象性质知:
当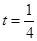 时,
时,
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
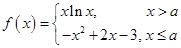 ,其中
,其中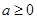 .
.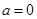 时,求函数
时,求函数 的图象在点
的图象在点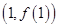 处的切线方程;
处的切线方程; 、
、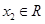 ,且
,且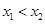 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.
 有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由;
有两个不同的极值点.其极小值为M,试比较2M与一3的大小,并说明理由; .
.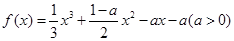 .
.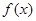 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围; .
. 的单调区间;
的单调区间;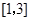 上的最值.
上的最值.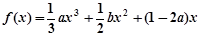 ,
, ,
,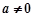 .
. 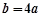 ,求
,求 的单调递增区间;
的单调递增区间;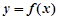 与
与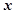 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且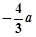 ,求
,求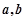 的值.
的值.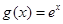 ,
,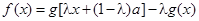 ,其中
,其中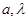 是常数,且
是常数,且 .
. 的极值;
的极值; ,存在正数
,存在正数 ,使不等式
,使不等式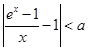 成立;
成立;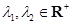 ,且
,且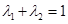 ,证明:对任意正数
,证明:对任意正数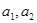 都有:
都有: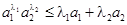 .
.