题目内容
过点M(2，1)的直线l与x轴，y轴分别交于不同的两点P，Q，且
则直线l的方程为_______．
答案：x＋2y－4=0#x－2y=0
解析：
解析：
|
解：设经过点 M的直线l的方程为m(x－2)＋n(y－1)=0，由于直线 l与坐标轴交于不同的两点，所以mn≠0，令 x=0，得 令y=0，得
从而有 
由  结合两点的距离公式，有
∴  整理得
从而有  ∴
∴所求直线 l的方程为m(x－2)±2m(y－1)=0，即x＋2y－4=0，或x－2y=0． |
练习册系列答案
相关题目
椭圆E：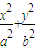
=1（a＞b＞0）离心率为
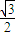，且过P（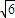
，
）．
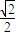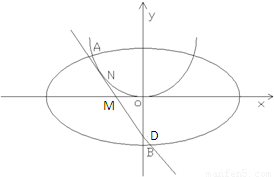
，0），且与开口朝上，顶点在原点的抛物线C切于第二象限的一点N，直 线l与椭圆E交于A，B两点，与y轴交与D点，若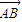
=
，
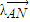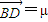
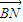，且λ+μ=
，求抛物线C的标准方程．