题目内容
(本小题满分12分)
设数列 对任意正整数n都成立,m为大于—1的非零常数。
对任意正整数n都成立,m为大于—1的非零常数。
(1)求证 是等比数列;
是等比数列;
(2设数列



求证:
见解析。
解析试题分析:(1)根据 ①
① (2),作差法得到其递推关系式,进而分析得到结论。
(2),作差法得到其递推关系式,进而分析得到结论。
(2) 由(1)知 ,得到
,得到 ,表示出通项公式,进而求和。
,表示出通项公式,进而求和。
(1)证明:由已知: ①
① ②
②
由①—②得
又∵m为大于—1的非零常数 
故 是等比数列。 ………………6分
是等比数列。 ………………6分
(2)解:当n=1时,
由(1)知

考点:本试题主要考查了等比数列的定义以及裂项求和的运用。
点评:解决该试题的关键是能利用通项公式与前n项和的关系式,来得到通项公式。同时利用递推关系整体的思想得到 ,同时裂项法得到求和。
,同时裂项法得到求和。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列 的通项公式是
的通项公式是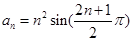 ,
,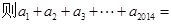 ( )
( )
A.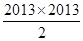 | B.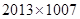 |
C. | D.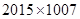 |
 的前
的前 项和为
项和为 ,
, 
 ,求
,求 ;
;  ,证明
,证明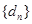 是等差数列.
是等差数列. 中,
中, 分别是某等差数列的第5项、第3项、第2项,且
分别是某等差数列的第5项、第3项、第2项,且 公比
公比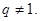
 满足:
满足: 的前n项和
的前n项和
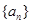 中,
中, ,并且对于任意n∈N*,都有
,并且对于任意n∈N*,都有 .
. 为等差数列,并求
为等差数列,并求 的前n项和为
的前n项和为 ,求使得
,求使得 的最小正整数
的最小正整数 .
.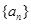 中,
中, .
.  分别为等差数列
分别为等差数列 的第4项和第16项,求数列
的第4项和第16项,求数列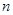 项和
项和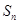 .
. 是首项为19,公差d=-2的等差数列,
是首项为19,公差d=-2的等差数列, 为
为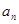 及
及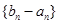 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列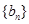 的通项公式及其前n项和
的通项公式及其前n项和
 的前
的前 项和为
项和为 且
且 .
. ;
; 问是否存在实数
问是否存在实数 ,使得对于任意的
,使得对于任意的 都有
都有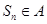 ? 若存在,求出
? 若存在,求出