题目内容
设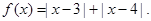
(Ⅰ)求函数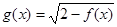 的定义域;
的定义域;
(Ⅱ)若存在实数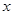 满足
满足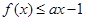 ,试求实数
,试求实数 的取值范围.
的取值范围.
(Ⅰ)[ ,
, ],(Ⅱ)(-∞,-2)∪[
],(Ⅱ)(-∞,-2)∪[ ,+∞).
,+∞).
解析试题分析:先将绝对值函数去绝对值,再求定义域,利用图像解不等式.
试题解析:(Ⅰ)f(x)=|x-3|+|x-4|= 2分
2分
作函数y=f(x)的图象,它与直线y=2交点的横坐标为 和
和 ,由图象知
,由图象知
不等式 的定义域为[
的定义域为[ ,
, ]. 5分
]. 5分

(Ⅱ)函数y=ax-1的图象是过点(0,-1)的直线.
当且仅当函数y=f(x)与直线y=ax-1有公共点时,存在题设的x.
由图象知,a取值范围为(-∞,-2)∪[ ,+∞). 10分
,+∞). 10分
考点:含绝对值式,求定义域,图像法解不等式.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
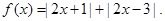
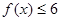 的解集;
的解集;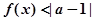 的解集非空,求实数
的解集非空,求实数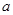 的取值范围.
的取值范围.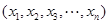 满足条件:
满足条件: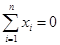 ; ②
; ②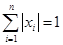 .
.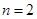 时,求
时,求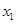 ,
,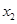 的值;
的值;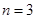 时,求证:
时,求证: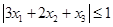 ;
;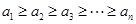 ,且
,且
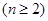 ,求证:
,求证: .
.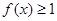 在区间(-∞,+∞)上恒成立,求实数a的取值范围
在区间(-∞,+∞)上恒成立,求实数a的取值范围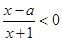 的解集为P,不等式
的解集为P,不等式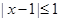 的解集为Q.
的解集为Q.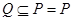 求正数a的取值范围
求正数a的取值范围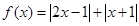 .
.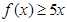 ;
;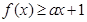 的解集为
的解集为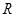 ,求实数
,求实数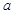 的取值范围.
的取值范围.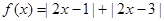 ,
,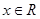 .
. ;
;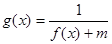 的定义域为
的定义域为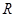 ,求实数
,求实数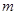 的取值范围.
的取值范围.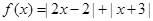 .
.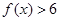 ;
; 的不等式
的不等式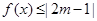 的解集不是空集,试求实数
的解集不是空集,试求实数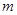 的取值范围.
的取值范围.