题目内容
定义在R上的奇函数 有最小正周期4,且
有最小正周期4,且 时,
时, 。
。
(1)求 在
在 上的解析式;
上的解析式;
(2)判断 在
在 上的单调性,并给予证明;
上的单调性,并给予证明;
(3)当 为何值时,关于方程
为何值时,关于方程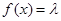 在
在 上有实数解?
上有实数解?
(1)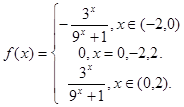 (2)
(2) 在(0,2)上单调递减;(3)
在(0,2)上单调递减;(3)
解析试题分析:(1)当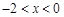 时,
时,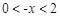 ,利用
,利用 时,
时, ,可得
,可得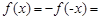
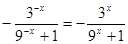 ,当
,当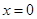 时,由
时,由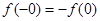 ,可得
,可得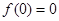 ,又
,又 的最小正周期4,可得
的最小正周期4,可得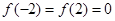 ,由此可求
,由此可求 在[-2,2]上的解析式;(2)直接利用函数单调性的定义去求;(3)利用
在[-2,2]上的解析式;(2)直接利用函数单调性的定义去求;(3)利用 在(0,2)上单调递减和
在(0,2)上单调递减和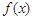 为奇函数,分别求出
为奇函数,分别求出 在
在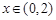 、
、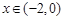 、
、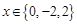 上的范围,从而得出
上的范围,从而得出 的取值范围.
的取值范围.
试题解析:(1)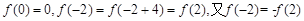
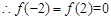 1分
1分
当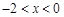 时,
时,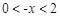 ,故
,故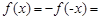
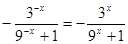 3分
3分 4分
4分
(2)任取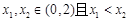 ,
,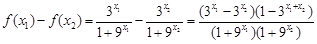 6分
6分
因为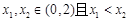 故
故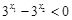 ,
,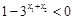 ,
,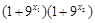 >0
>0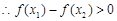 故
故 在(0,2)上单调递减。 8分
在(0,2)上单调递减。 8分
(3)由(2)知: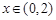 时,
时,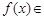

又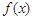 为奇函数,
为奇函数,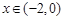 时,
时,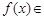
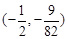
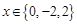 时,
时,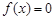
综上:  12分
12分
考点:函数奇偶性的性质;函数解析式的求解及常用方法;函数的周期性,函数的单调性.

练习册系列答案
相关题目
 长为2m,跳水板距水面
长为2m,跳水板距水面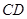 的高
的高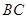 为3m,
为3m, =5m,
=5m,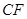 =6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点
=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点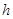 m(
m(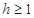 )时达到距水面最大高度4m,规定:以
)时达到距水面最大高度4m,规定:以 为纵轴建立直角坐标系.
为纵轴建立直角坐标系.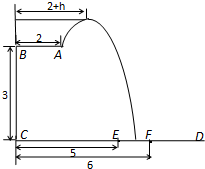
 内入水时才能达到压水花的训练要求,求达到压水花的训练要求时
内入水时才能达到压水花的训练要求,求达到压水花的训练要求时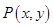 为函数
为函数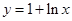 图象上一点,
图象上一点, 为坐标原点,记直线
为坐标原点,记直线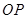 的斜率
的斜率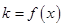 .
.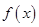 在区间
在区间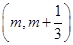
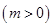 上存在极值,求实数
上存在极值,求实数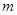 的取值范围;
的取值范围;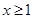 时,不等式
时,不等式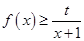 恒成立,求实数
恒成立,求实数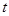 的取值范围;
的取值范围;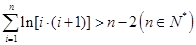 .
. .设某商品标价为
.设某商品标价为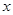 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为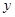 .
. 时,
时,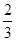 ?
?
 .
. 在定义域上为增函数,求实数
在定义域上为增函数,求实数 的取值范围;
的取值范围; 上的最小值.
上的最小值. ,
,
 .
. 的解集;
的解集; 的不等式
的不等式 在
在 的取值范围.
的取值范围. ,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.
,其中a是实数,设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的点,且x1<x2.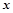 (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车速度为0;当车流密度不超过20辆/千米时,车流速度为60千米,/小时,研究表明:当 时,车流速度v是车流密度
时,车流速度v是车流密度 时,求函数
时,求函数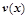 的表达式;
的表达式; 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)