题目内容
设函数 ,
,
 .
.
⑴ 求不等式 的解集;
的解集;
⑵ 如果关于 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(1) (2)
(2)
解析试题分析:(1)利用分类讨论思想去掉绝对值,得到分段函数,逐一求解;(2)构造函数 采用数形结合思想,借助两个函数图象进行比较分析.
采用数形结合思想,借助两个函数图象进行比较分析.
试题解析:(1) 
 (2分)
(2分)
当 时,
时, ,
, ,则
,则 ;
;
当 时,
时, ,
, ,则
,则 ;
;
当  时,
时, ,
, ,则
,则 .
.
综上可得,不等式的解集为 . (5分)
. (5分)
(2) 设 ,由函数
,由函数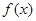 的图像与
的图像与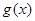 的图像可知:
的图像可知: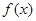 在
在 时取最小值为6,
时取最小值为6,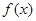 在
在 时取最大值为
时取最大值为 ,
,
若 恒成立,则
恒成立,则 . (10分)
. (10分)
考点:1.不等式的相关知识;2.绝对值不等式;3.不等式证明.

练习册系列答案
相关题目
 名工人,现接受了生产
名工人,现接受了生产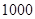 台
台 型高科技产品的总任务.已知每台
型高科技产品的总任务.已知每台 个
个 型装置和
型装置和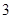 个
个 型装置配套组成,每个工人每小时能加工
型装置配套组成,每个工人每小时能加工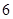 个
个 人,他们加工完
人,他们加工完 ,其余工人加工完
,其余工人加工完 (单位:小时,可不为整数).
(单位:小时,可不为整数). 的解析式;
的解析式; 为偶函数,且在区间
为偶函数,且在区间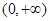 上是单调增函数.
上是单调增函数. 的解析式;
的解析式; ,若
,若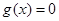 的两个实根分别在区间
的两个实根分别在区间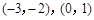 内,求实数
内,求实数 的取值范围.
的取值范围. 有最小正周期4,且
有最小正周期4,且 时,
时, 。
。 上的解析式;
上的解析式; 上的单调性,并给予证明;
上的单调性,并给予证明; 为何值时,关于方程
为何值时,关于方程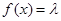 在
在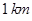 的等边三角形
的等边三角形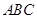 的顶点
的顶点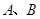 处(如图),现要在边
处(如图),现要在边 上的
上的 点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返
点建一仓库,某工人每天用叉车将生产原料从仓库运往车间,同时将成品运回仓库.已知叉车每天要往返 车间5次,往返
车间5次,往返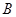 车间20次,设叉车每天往返的总路程为
车间20次,设叉车每天往返的总路程为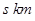 .(注:往返一次即先从仓库到车间再由车间返回仓库)
.(注:往返一次即先从仓库到车间再由车间返回仓库)
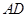 长为
长为 ,将
,将 表示成
表示成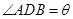 ,将
,将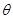 的函数关系式.
的函数关系式.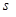 的最小值,并指出点
的最小值,并指出点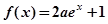 ,
,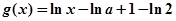 ,其中
,其中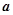 为常数,
为常数,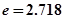 ,函数
,函数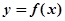 的图象与坐标轴交点处的切线为
的图象与坐标轴交点处的切线为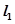 ,函数
,函数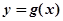 的图象与直线
的图象与直线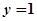 交点处的切线为
交点处的切线为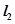 ,且
,且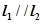 。
。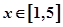 ,不等式
,不等式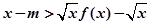 成立,求实数
成立,求实数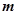 的取值范围.
的取值范围.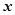 。我们把
。我们把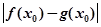 的值称为两函数在
的值称为两函数在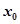 处的偏差。求证:函数
处的偏差。求证:函数 的最大值;
的最大值;  是否有实数解 .
是否有实数解 .