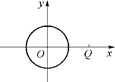
题目内容
如图,设椭圆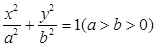 的左、右焦点分别为
的左、右焦点分别为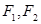 ,点
,点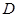 在椭圆上,
在椭圆上,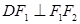 ,
, ,
,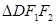 的面积为
的面积为 .
.
(1)求该椭圆的标准方程;
(2)是否存在圆心在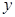 轴上的圆,使圆在
轴上的圆,使圆在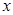 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.

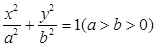 的左、右焦点分别为
的左、右焦点分别为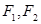 ,点
,点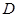 在椭圆上,
在椭圆上,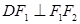 ,
, ,
,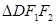 的面积为
的面积为 .
.(1)求该椭圆的标准方程;
(2)是否存在圆心在
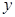 轴上的圆,使圆在
轴上的圆,使圆在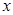 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
(1)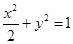 ;(2)存在满足条件的圆,其方程为
;(2)存在满足条件的圆,其方程为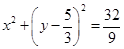 .
.
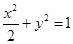 ;(2)存在满足条件的圆,其方程为
;(2)存在满足条件的圆,其方程为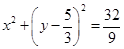 .
.试题分析:(1)由题设知
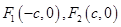 其中
其中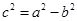
由
 ,结合条件
,结合条件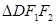 的面积为
的面积为 ,可求
,可求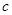 的值,再利用椭圆的定义和勾股定理即可求得
的值,再利用椭圆的定义和勾股定理即可求得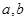 的值,从而确定椭圆的标准方程;
的值,从而确定椭圆的标准方程;(2)假设存在圆心在
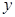 轴上的圆,使圆在
轴上的圆,使圆在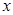 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点;设圆心在
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点;设圆心在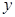 轴上的圆与椭圆在
轴上的圆与椭圆在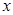 轴的上方有两个交点为
轴的上方有两个交点为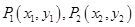 由圆的对称性可知
由圆的对称性可知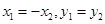 ,利用
,利用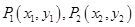 在圆上及
在圆上及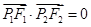 确定交点的坐标,进而得到圆的方程.
确定交点的坐标,进而得到圆的方程.解:(1)设
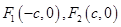 ,其中
,其中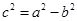 ,
,由
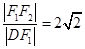 得
得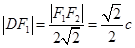
从而
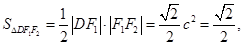 故
故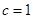 .
.从而
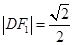 ,由
,由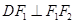 得
得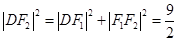 ,因此
,因此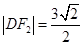 .
.所以
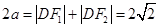 ,故
,故
因此,所求椭圆的标准方程为:
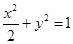
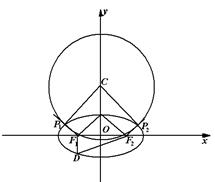
(2)如图,设圆心在
 轴上的圆
轴上的圆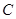 与椭圆
与椭圆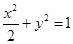 相交,
相交,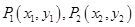 是两个交点,
是两个交点,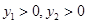 ,
,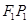 ,
,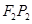 是圆
是圆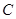 的切线,且
的切线,且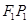
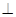
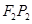 由圆和椭圆的对称性,易知
由圆和椭圆的对称性,易知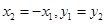
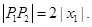 ,
, 由(1)知
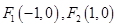 ,所以
,所以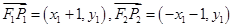 ,再由
,再由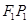
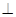
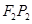 得
得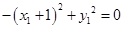 ,由椭圆方程得
,由椭圆方程得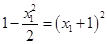 ,即
,即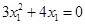 ,解得
,解得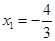 或
或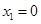 .
.当
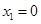 时,
时,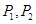 重合,此时题设要求的圆不存在.
重合,此时题设要求的圆不存在.当
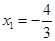 时,过
时,过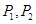 分别与
分别与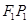 ,
,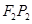 垂直的直线的交点即为圆心
垂直的直线的交点即为圆心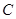 ,设
,设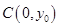
由
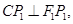 得
得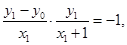 而
而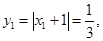 故
故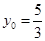
圆
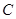 的半径
的半径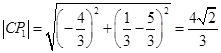
综上,存在满足条件的圆,其方程为:
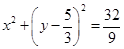

练习册系列答案
相关题目
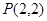 ,圆
,圆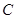 :
: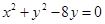 ,过点
,过点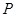 的动直线
的动直线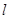 与圆
与圆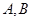 两点,线段
两点,线段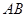 的中点为
的中点为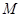 ,
,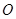 为坐标原点.
为坐标原点.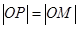 时,求
时,求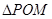 的面积
的面积 与⊙O的交点.若
与⊙O的交点.若 ,
, ,求证:
,求证: .
.
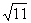 为半径的圆
为半径的圆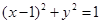 上异于坐标原点O的任意一点,直线OP的倾斜角为 ,若
上异于坐标原点O的任意一点,直线OP的倾斜角为 ,若 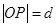 ,则函数
,则函数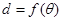 的大致图像是 ( )
的大致图像是 ( )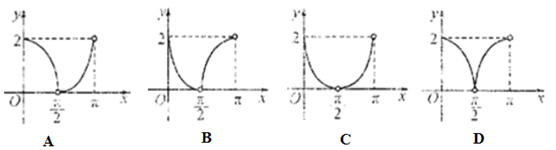
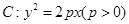 上一点
上一点 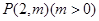 ,若P到焦点F的距离为4,则以P为圆心且与抛物线C的准线相切的圆的标准方程为_________.
,若P到焦点F的距离为4,则以P为圆心且与抛物线C的准线相切的圆的标准方程为_________.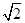 .求动点M的轨迹方程,并说明它表示什么.
.求动点M的轨迹方程,并说明它表示什么.