Question

已知一等比数列前n项和为2,其后2n项的和为12,求再后面3n项的和.

     

Answer 1

思路分析:此题已知S_n=2,S_3n-S_n=12,根据求和公式可列出关于a₁和q的两个方程组成的方程组,解出a₁和q,但是较繁琐,若注意到所求式与已知表达式之间的关系,会发现只要求出qⁿ即可,不需求出q,另外,也可用等比数列的性质解题,S_n,S_2n-S_n,S_3n-S_2n构成新数列,使问题简化.

    解法一:利用求和公式求解,设S=a_3n+1+a_3n+2+…+a_6n.

∵S_n=2,若公比q=1,那么紧接着后面的2n项的和应为S_3n-S_n=2×3-2=4,而不是12,∴q≠1.

    由题设得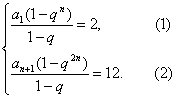

可得q²ⁿ+qⁿ-6=0.

    解之,得qⁿ=2或qⁿ=-3.

S=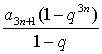=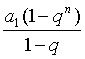·q³ⁿ(1+qⁿ+q²ⁿ),

    当n为偶数时,qⁿ=2,S=112;当n为奇数时,qⁿ=2或qⁿ=-3,S=112或S=-378.

    解法二:利用等比数列的性质求解.设S=a_3n+1+a_3n+2+…+a_6n,

    由已知a₁+a₂+…+a_n=2,a_n+1+a_n+2+…+a_2n+a_2n+1+a_2n+2+…+a_3n=12.

    注意到(a₁+a₂+…+a_n),(a_n+1+a_n+2+…+a_2n),(a_2n+1+a_2n+2+…+a_3n),(a_3n+1+a_3n+2+…+a_4n),…也成等比数列,其公比为qⁿ,于是,问题转化为已知A₁=2,A₁qⁿ+A₁q²ⁿ=12,要求A₁q³ⁿ+A₁q⁴ⁿ+A₁q⁵ⁿ的值.

    由A₁=2,A₁qⁿ+A₁q²ⁿ=12,得q²ⁿ+qⁿ-6=0,∴qⁿ=2或qⁿ=-3.

    故S=A₁q³ⁿ+A₁q⁴ⁿ+A₁q⁵ⁿ=A₁q³ⁿ(1+qⁿ+q²ⁿ)=2·q³ⁿ·7=14q³ⁿ.

    当n为偶数时,qⁿ=2,此时S=14·(qⁿ)³=112;当n为奇数时,qⁿ=2或qⁿ=-3,此时S=14·(qⁿ)³=112或S=14·(qⁿ)³=14×(-3)³=-378.

    解法三:(利用等比数列的性质求解)设S=a_3n+1+a_3n+2+…+a_6n,

    等比数列{a_n}中,A₁=a₁+a₂+…+a_n,

A₂=a_n+1+…+a_2n,

A₃=a_2n+1+a_2n+2+…+a_3n,

A₄=a_3n+1+a_3n+2+…+a_4n,

A₅=a_4n+1+a_4n+2+…+a⁵ⁿ,

A₆=a⁵ⁿ⁺¹+a⁵ⁿ⁺²+…+a_6n.

    由等比数列的性质可知A₁,A₂,A₃,…,A₅,A₆构成等比数列,且设其公比为Q,由已知条件可得A₂+A₃=12,即A₁Q+A₁Q²=12,解得Q=2或Q=-3.

    由于Q==qⁿ,故当n为偶数时,qⁿ＞0,即Q＞0,

∴Q=2,此时S=A₄+A₅+A₆=A₁Q³+A₁Q⁴+A₁Q⁵=2×(2³+2⁴+2⁵)=112.

    当n为奇数时,Q=2或Q=-3,此时,S=A₄+A₅+A₆=A₁(Q³+Q⁴+Q⁵)=112或

S=A₄+A₅+A₆=A₁(Q³+Q⁴+Q⁵)=-378.