题目内容
已知椭圆的中心在原点，焦点在y轴上且长轴长为4，短轴长为2，直线l的参数方程为
(t为参数).当m为何值时，直线l被椭圆截得的弦长为
?
解析：在利用直线的参数方程求弦长时,先将参数方程代入二次曲线的普通方程,得关于t的二次方程At2+Bt+C=0,则弦长为
|t1-t2|=
解：椭圆方程为+x2=1,
化直线参数方程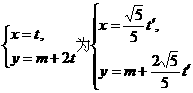
(t′为参数).
代入椭圆方程得(m+
)2+4(
t′)2=4
8t′2+4
mt′+5m2-20=0.
当Δ=80m2-160m2+640=640-80m2＞0,即-2
＜m＜2
时，方程有两不等实根t′1、t′2,则弦长为|t′1-t′2|=
依题意知
.解之，得m=±
.
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目