题目内容
给出函数f(x)=arccos(sinx),那么
- A.

- B.

- C.

- D.

B
分析:根据y=sinx在(- ,
, )上是增函数,y=arccosx在(-1,1)上是减函数,可得y=arccos(sinx)在
)上是增函数,y=arccosx在(-1,1)上是减函数,可得y=arccos(sinx)在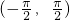 上是减函数,由此得出结论.
上是减函数,由此得出结论.
解答:∵y=sinx在(- ,
, )上是增函数,y=arccosx在(-1,1)上是减函数,
)上是增函数,y=arccosx在(-1,1)上是减函数,
∴y=arccos(sinx)在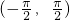 上是减函数,故有
上是减函数,故有 ,
,
故选B.
点评:本题主要考查反三角函数的应用,正弦函数的单调性、反余弦函数的单调性、复合函数的单调性的应用,属于基础题
分析:根据y=sinx在(-
 ,
, )上是增函数,y=arccosx在(-1,1)上是减函数,可得y=arccos(sinx)在
)上是增函数,y=arccosx在(-1,1)上是减函数,可得y=arccos(sinx)在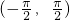 上是减函数,由此得出结论.
上是减函数,由此得出结论.解答:∵y=sinx在(-
 ,
, )上是增函数,y=arccosx在(-1,1)上是减函数,
)上是增函数,y=arccosx在(-1,1)上是减函数,∴y=arccos(sinx)在
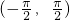 上是减函数,故有
上是减函数,故有 ,
,故选B.
点评:本题主要考查反三角函数的应用,正弦函数的单调性、反余弦函数的单调性、复合函数的单调性的应用,属于基础题

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

 (2012•昌图县模拟)给出函数f(x)=3sin(ωx+φ) (ω>0,|φ|<
(2012•昌图县模拟)给出函数f(x)=3sin(ωx+φ) (ω>0,|φ|< (2007•温州一模)设函数y=f(x),我们把满足方程f(x)=0的值x叫做函数y=f(x)的零点.现给出函数f(x)=x3-3x2+ax+a2-10,若它是R上的单调函数,且1是它的零点.
(2007•温州一模)设函数y=f(x),我们把满足方程f(x)=0的值x叫做函数y=f(x)的零点.现给出函数f(x)=x3-3x2+ax+a2-10,若它是R上的单调函数,且1是它的零点.