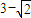题目内容
过双曲线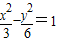 的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,O为坐标原点,F1为左焦点.
的右焦点F2,倾斜角为30°的直线交双曲线于A,B两点,O为坐标原点,F1为左焦点.(1)求|AB|;
(2)求△AOB的面积;
(3)求证:|AF2|+|BF2|=|AF1|+|BF1|.
【答案】分析:(1)根据双曲线的标准方程,确定焦点坐标,进而可得直线AB的方程,与双曲线联立,利用韦达定理,可计算|AB|;
(2)求出原点O到直线AB的距离,即可求得△AOB的面积;
(3)利用双曲线的定义,即可证得结论.
解答: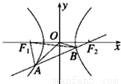 (1)解:由双曲线的方程得a=
(1)解:由双曲线的方程得a=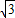 ,b=
,b=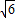 ,
,
∴c=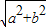 =3,F1(-3,0),F2(3,0).
=3,F1(-3,0),F2(3,0).
∴直线AB的方程为y=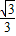 (x-3).
(x-3).
设A(x1,y1),B(x2,y2),由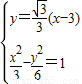 得5x2+6x-27=0.
得5x2+6x-27=0.
∴x1+x2=- ,x1x2=-
,x1x2=-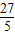 .
.
∴|AB|=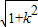 |x1-x2|=
|x1-x2|=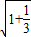 •
•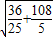 =
=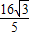
(2)解:直线AB的方程变形为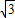 x-3y-3
x-3y-3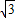 =0.
=0.
∴原点O到直线AB的距离为d=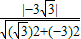 =
= .
.
∴S△AOB= |AB|•d=
|AB|•d= ×
×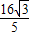 ×
× =
=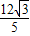 .…(8分)
.…(8分)
(3)证明:如图,由双曲线的定义得
|AF2|-|AF1|=2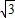 ,|BF1|-|BF2|=2
,|BF1|-|BF2|=2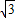 ,
,
∴|AF2|+|BF2|=|AF1|+|BF1|…(12分)
点评:本题考查双曲线的几何性质,考查直线与双曲线的位置关系,考查双曲线的定义,考查学生的计算能力,属于中档题.
(2)求出原点O到直线AB的距离,即可求得△AOB的面积;
(3)利用双曲线的定义,即可证得结论.
解答:
 (1)解:由双曲线的方程得a=
(1)解:由双曲线的方程得a=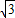 ,b=
,b=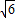 ,
,∴c=
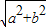 =3,F1(-3,0),F2(3,0).
=3,F1(-3,0),F2(3,0).∴直线AB的方程为y=
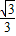 (x-3).
(x-3).设A(x1,y1),B(x2,y2),由
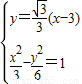 得5x2+6x-27=0.
得5x2+6x-27=0.∴x1+x2=-
 ,x1x2=-
,x1x2=-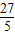 .
.∴|AB|=
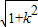 |x1-x2|=
|x1-x2|=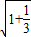 •
•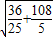 =
=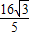
(2)解:直线AB的方程变形为
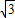 x-3y-3
x-3y-3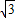 =0.
=0.∴原点O到直线AB的距离为d=
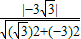 =
= .
.∴S△AOB=
 |AB|•d=
|AB|•d= ×
×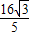 ×
× =
=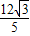 .…(8分)
.…(8分)(3)证明:如图,由双曲线的定义得
|AF2|-|AF1|=2
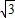 ,|BF1|-|BF2|=2
,|BF1|-|BF2|=2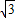 ,
,∴|AF2|+|BF2|=|AF1|+|BF1|…(12分)
点评:本题考查双曲线的几何性质,考查直线与双曲线的位置关系,考查双曲线的定义,考查学生的计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
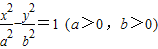 的右焦点F2作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B.若
的右焦点F2作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B.若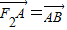 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( ) 的右焦点F2,作倾斜角为
的右焦点F2,作倾斜角为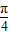 的直线交双曲线于A、B两点,
的直线交双曲线于A、B两点, 的右焦点F2作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B.若
的右焦点F2作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为A,B.若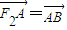 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( ) 的右焦点F2作垂直于实轴的弦PQ,F1是左焦点,若∠PF1Q=90°,则双曲线的离心率是( )
的右焦点F2作垂直于实轴的弦PQ,F1是左焦点,若∠PF1Q=90°,则双曲线的离心率是( )