题目内容
【题目】已知动圆过定点
，且与定直线
相切.
（1）求动圆圆心的轨迹
的方程；
（2）若
是轨迹的动弦，且过， 分别以
、
为切点作轨迹的切线，设两切线交点为
，证明:
.
【答案】（1）
（2）详见解析
【解析】
试题（I）由题意可得：动圆圆心到定点（0，2）与到定直线y=-2的距离相等，利用抛物线的定义求轨迹方程即可；（II）设AB：y=kx+2，将直线的方程代入抛物线的方程，消去y得到关于x的一元二次方程，再结合根与系数的关系利用切线的几何意义即可求得过抛物线上A、B两点的切线斜率关系，从而解决问题
试题解析：（1）依题意，圆心的轨迹是以
为焦点，
为准线的抛物线
因为抛物线焦点到准线距离等于4, 所以圆心的轨迹方程是
（2）
， 
，
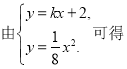
抛物线方程为
所以过抛物线上A、B两点的切线斜率分别是
，
.
所以，
(注:也可设
,再由
,设
则直线AQ:
,联立直线和抛物线方程,由直线和抛物线相切得
可得，同理可得，从而证
）
阅读快车系列答案【题目】某高校为调查学生喜欢“应用统计”课程是否与性别有关，随机抽取了选修课程的55名学生，得到数据如下表：
喜欢统计课程 | 不喜欢统计课程 | |
男生 | 20 | 5 |
女生 | 10 | 20 |
临界值参考：
| 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：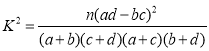
，其中
）
参照附表，得到的正确结论是（ ）
A.在犯错误的概率不超过
的前提下，认为“喜欢“应用统计”课程与性别有关”
B.在犯错误的概率不超过的前提下，认为“喜欢“应用统计”课程与性别无关”
C.有
以上的把握认为“喜欢应用统计”课程与性别有关”
D.有以上的把握认为“喜欢“应用统计”课程与性别无关”
【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)
男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:
，
，
，
，
，
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
