题目内容
(本小题满分14分)已知函数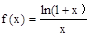
(1)确定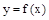 在(0,+
在(0,+ )上的单调性;
)上的单调性;
(2)设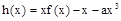 在(0,2)上有极值,求a的取值范围.
在(0,2)上有极值,求a的取值范围.
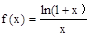
(1)确定
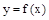 在(0,+
在(0,+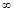 )上的单调性;
)上的单调性;(2)设
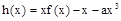 在(0,2)上有极值,求a的取值范围.
在(0,2)上有极值,求a的取值范围.解:(1)由题知 .
.
设
则 在(0,+
在(0,+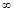 )恒成立,
)恒成立,
∴g(x)在(0,+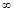 )上单调递减,
)上单调递减,
∴g(x)<g(0)="0, " ∴ .
.
因此 在(0,+
在(0,+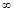 )上单调递减。
)上单调递减。
(2)由 可得,
可得,
 ,
,
若 ,对任意
,对任意 ,
,
∴h(x)在(0,2)上单调递减,则f(x)在(0,2)上无极值。
若a<0, 在(0,2)上有极值的充要条件是
在(0,2)上有极值的充要条件是 在(0,2)上有零点,
在(0,2)上有零点,
又 在(-
在(- 上单调,
上单调,
∴
综上,a的取值范围是(- ).
).
 .
.设

则
 在(0,+
在(0,+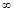 )恒成立,
)恒成立,∴g(x)在(0,+
 )上单调递减,
)上单调递减,∴g(x)<g(0)="0, " ∴
 .
.因此
 在(0,+
在(0,+ )上单调递减。
)上单调递减。(2)由
 可得,
可得, ,
,若
 ,对任意
,对任意 ,
,∴h(x)在(0,2)上单调递减,则f(x)在(0,2)上无极值。
若a<0,
 在(0,2)上有极值的充要条件是
在(0,2)上有极值的充要条件是 在(0,2)上有零点,
在(0,2)上有零点,又
 在(-
在(- 上单调,
上单调,∴

综上,a的取值范围是(-
 ).
).略

练习册系列答案
相关题目
 ,其中
,其中 ,b∈R且b≠0。
,b∈R且b≠0。 的单调区间;
的单调区间; 没有实根,求a的取值范围;
没有实根,求a的取值范围; ,其中
,其中 .
. 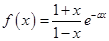

 ,讨论
,讨论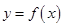 的单调性;
的单调性;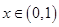 恒有
恒有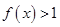 ,求
,求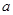 的取值范围
的取值范围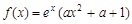
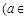 R).
R).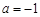 ,求曲线
,求曲线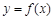 在点
在点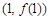 处的的切线方程;
处的的切线方程; 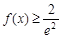 对任意
对任意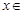
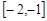 恒成立,求实数
恒成立,求实数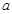 的取值范围.
的取值范围.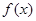 对
对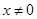 的任意实数,恒有
的任意实数,恒有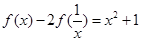 成立.
成立.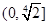 上是增函数
上是增函数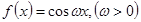 将
将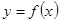 的图象向右平移
的图象向右平移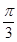 个单位长
个单位长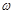 的最小值等于( )
的最小值等于( )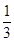
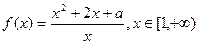
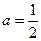 时,求函数
时,求函数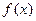 的最小值;
的最小值;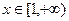 ,
,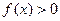 恒成立,试求实数
恒成立,试求实数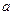 的取值范围.
的取值范围. (x+
(x+ -a)的定义域为A,值域为B.
-a)的定义域为A,值域为B. 的图象与直线
的图象与直线 相切,则a等于( )
相切,则a等于( )

