题目内容
(2006
北京朝阳模拟)如图所示,已知圆 ,设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
,设M为圆C与x轴负半轴的交点,过M作圆C的弦MN,并使它的中点P恰好落在y轴上.
(1)
当r=2时,求满足条件的P点的坐标;(2)
当r (1,+∞)时,求点N的轨迹G的方程;
(1,+∞)时,求点N的轨迹G的方程;
(3)
过点P(0,2)的直线l与(2)中轨迹G相交于两个不同的点E、F,若 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.

答案:略
解析:
解析:
|
解析: (1)解法一:由已知得,r=2时,可求得M点的坐标为M(-1,0).设 P(0,b),则由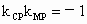 . .
( 或用勾股定理)得 . .
∴ b=±1,即点P坐标为(0,±1).解法二:同上可得 M(-1,0)设N(x,y),则
解得 N(1,±2).∴ MN的中点P坐标为(0,±1),(2) 解法一:设N(x,y),由已知得,在圆方程中令 y=0,求得M点的坐标为(1-r,0).设 P(0,b),则由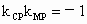 . .
( 或用 ) )
∵点 P为线段MN的中点,∴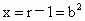 ,y=2b.又r>1, ,y=2b.又r>1,
∴点 N的轨迹方程为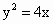 (x≠0). (x≠0).
解法二:设 N(x,y),同上可得 M(1-r,0),则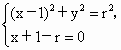 ,消去r,又r>1, ,消去r,又r>1,
∴点 N的轨迹方程为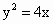 (x≠0). (x≠0).
(3) 依题意得直线l的斜率存在且不为0,设直线l的方程为y=kx+2,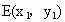 , ,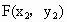 , ,
由  ,得 ,得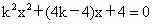 . .
由Δ =-32k+16>0,得 . .
∵  , ,
∴ 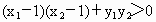 . .
∴ 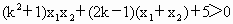 . .
得 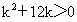 . .
∴ k>0或k<-12.∴ 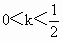 或k<-12. 或k<-12. |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(2006
北京朝阳模拟)下列函数中,最小正周期为π,且图象关于直线 对称的是
对称的是
[
]|
A . |
B . |
|
C . |
D . |
(2006
北京朝阳模拟)如下图,正方体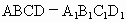 中,E、F分别是棱
中,E、F分别是棱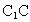 与BC的中点,则直线EF与直线
与BC的中点,则直线EF与直线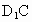 所成角的大小是
所成角的大小是
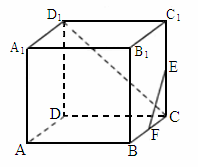
[
]|
A .45° |
B .60° |
|
C .75° |
D .90° |
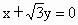 绕原点按顺时针方向旋转30°,所得直线与圆
绕原点按顺时针方向旋转30°,所得直线与圆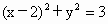 的位置关系是
的位置关系是
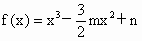 ,1<m<2.
,1<m<2.
 ,试判断函数F(x)的极值点个数,并求出相应实数m的范围.
,试判断函数F(x)的极值点个数,并求出相应实数m的范围.