题目内容
13.下列命题为真命题的是( )| A. | ?x∈N,x3>x2 | |
| B. | 函数f(x)=ax2+bx+c为偶函数的充要条件是b=0 | |
| C. | ?x0∈R,x02+2x0+2≤0 | |
| D. | “x>3”是“x2>9”的必要条件 |
分析 由x=0,1可得x3=x2,即可判断A;由偶函数的定义和充分必要条件的定义,可判断B;
由配方法和非负数,即可判断C;由充分必要条件的定义和不等式的解法即可判断D.
解答 解:对于A,当x=0或1时,x3=x2=0或1,则?x∈N,x3>x2为假命题;
对于B,函数f(x)=ax2+bx+c为偶函数,可得f(-x)=f(x),求得b=0,反之b=0,可得f(x)为偶函数
故充要条件是b=0,则B为真命题;
对于C,x02+2x0+2=(x0+1)2+1>0,则?x0∈R,x02+2x0+2≤0为假命题;
对于D,“x>3”是“x2>9?x>3或x<-3”的充分条件,故为假命题.
故选:B.
点评 本题考查命题的真假判断,主要考查充分必要条件的判断和全称命题和特称命题的真假,注意运用定义法和反例法,考查判断能力,属于基础题.

练习册系列答案
相关题目
19.某空间几何体的三视图如图所示,则该几何体的体积是( )


| A. | 32 | B. | 32$\sqrt{2}$ | C. | $\frac{32}{3}$ | D. | $\frac{32}{3}$$\sqrt{2}$ |
4.已知点A,B分别是椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{20}$=1长轴的左、右顶点,点F是椭圆的右焦点,点P在椭圆上,且位于x轴上方,PA⊥PF.设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,椭圆上的点到点M的距离d的最小值( )
| A. | $\frac{4\sqrt{3}}{5}$ | B. | $\sqrt{15}$ | C. | -1 | D. | 1 |
3.设m,n,l为空间不重合的直线,α,β,γ是空间不重合的平面,则下列说法正确的是( )
| A. | 若m⊥l,n⊥l,则m∥n | B. | 若l∥m,l?α,则α∥β | ||
| C. | 若m∥l,m∥α,则l∥α | D. | 若α⊥γ,β⊥γ,α∩β=l,则l⊥γ |
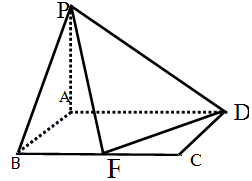 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是线段BC的中点
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是线段BC的中点