Question

【题目】已知向量 =（1，0）， =（m，1），且 与 的夹角为 ．
（1）求| ﹣2 |；
（2）若（ +λ ）与 垂直，求实数λ的值．

Answer 1

【答案】
（1）解：∵ =（1，0）， =（m，1），且 与 的夹角为 ．

∴ =m，| |=1，| |= ，

cos＜ ＞= = ，解得m=1，或m=﹣1（舍）

∴ =（﹣1，﹣2），

∴| ﹣2 |= =

（2）解：∵ =（1+λ，λ），

（ +λ ）与 垂直，

∴ ，

解得

【解析】（1）由cos＜ ＞= = ，求出m=1，由此能求出| ﹣2 |．（2）由 =（1+λ，λ），（ +λ ）与 垂直，能求出实数λ的值．
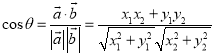【考点精析】本题主要考查了数量积表示两个向量的夹角和数量积判断两个平面向量的垂直关系的相关知识点，需要掌握设、都是非零向量，，，是与的夹角，则；若平面的法向量为，平面的法向量为，要证，只需证，即证;即：两平面垂直两平面的法向量垂直才能正确解答此题．