题目内容
当曲线y=1+
与直线kx-y-3k+4=0有两个相异的交点时,实数k的取值范围是( )
| 9-x2 |
分析:由条件化简可得半圆(图中红线)和直线有两个相异的交点,如图所示,求出NA、BC的斜率,可得实数k的取值范围.
解答: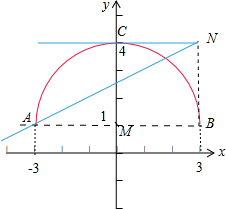 解:曲线y=1+
解:曲线y=1+
,即x2+(y-1)2=9(y≥1),
表示以M(0,1)为圆心,半径等于3的一个半圆.
直线kx-y-3k+4=0即 k(x-3)-y+4=0,经过定点N(3,4).
再根据半圆(图中红线)和直线有两个相异的交点,如图所示:
由题意可得,A(-3,1)、B(-3,1)、C(0,4),
直线NC和半圆相切,NA和半圆相较于两个点.
求得NA的斜率为
=
,NC的斜率为0,
故所求的实数k的范围为( 0,
],
故选C.
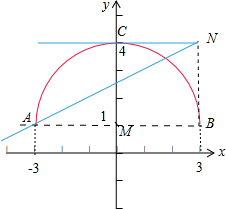 解:曲线y=1+
解:曲线y=1+| 9-x2 |
表示以M(0,1)为圆心,半径等于3的一个半圆.
直线kx-y-3k+4=0即 k(x-3)-y+4=0,经过定点N(3,4).
再根据半圆(图中红线)和直线有两个相异的交点,如图所示:
由题意可得,A(-3,1)、B(-3,1)、C(0,4),
直线NC和半圆相切,NA和半圆相较于两个点.
求得NA的斜率为
| 4-1 |
| 3-(-3) |
| 1 |
| 2 |
故所求的实数k的范围为( 0,
| 1 |
| 2 |
故选C.
点评:本题主要考查圆的标准方程,直线和圆的位置关系的应用,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目