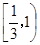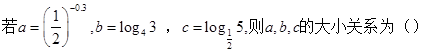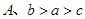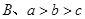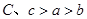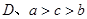题目内容
定义:若函数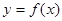 在某一区间D上任取两个实数
在某一区间D上任取两个实数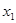 、
、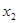 ,且
,且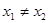 ,都有
,都有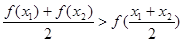 ,则称函数
,则称函数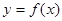 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数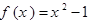 ,判断其在区间
,判断其在区间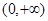 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数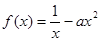 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数 的取值范围。
的取值范围。
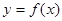 在某一区间D上任取两个实数
在某一区间D上任取两个实数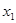 、
、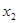 ,且
,且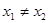 ,都有
,都有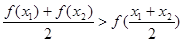 ,则称函数
,则称函数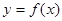 在区间D上具有性质L。
在区间D上具有性质L。(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数
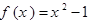 ,判断其在区间
,判断其在区间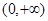 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。(3)若函数
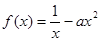 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数 的取值范围。
的取值范围。(1)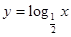 (2)有,证明见解析(3)
(2)有,证明见解析(3)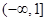
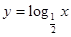 (2)有,证明见解析(3)
(2)有,证明见解析(3)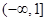
本题以函数为载体,考查新定义,考查恒成立问题,解题的关键是对新定义的理解,恒成立问题采用分离参数法.
(1)写出的函数是下凹的函数即可;
(2)函数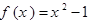 在区间
在区间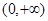 上具有性质L,运用定义法加以证明即可。
上具有性质L,运用定义法加以证明即可。
(3)任取x1、x2∈(0,1),且x1≠x2则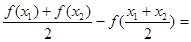 >0,只需要
>0,只需要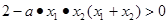 在x1、x2∈(0,1)上恒成立,故可求实数a的取值范围.
在x1、x2∈(0,1)上恒成立,故可求实数a的取值范围.
解:(1)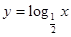 (或其它底在(0,1)上的对数函数)。…………2分
(或其它底在(0,1)上的对数函数)。…………2分
(2)函数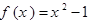 在区间
在区间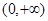 上具有性质L。…………3分
上具有性质L。…………3分
证明:任取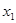 、
、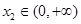 ,且
,且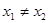
则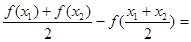
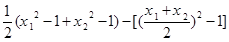
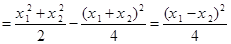

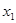 、
、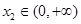 且
且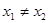 ,
,
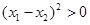 ,
,
即 >0,
>0,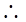
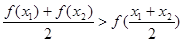
所以函数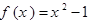 在区间
在区间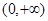 上具有性质L。……………7分
上具有性质L。……………7分
(3)任取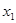 、
、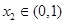 ,且
,且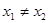
则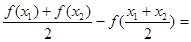
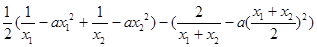
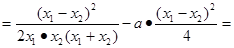
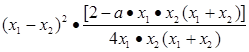

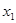 、
、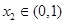 且
且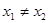 ,
,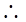
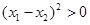 ,
,
要使上式大于零,必须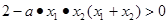 在
在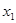 、
、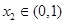 上恒成立,
上恒成立,
即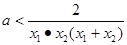 ,
,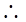
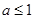 ,即实数
,即实数 的取值范围为
的取值范围为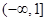 ……………12分
……………12分
(1)写出的函数是下凹的函数即可;
(2)函数
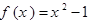 在区间
在区间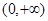 上具有性质L,运用定义法加以证明即可。
上具有性质L,运用定义法加以证明即可。(3)任取x1、x2∈(0,1),且x1≠x2则
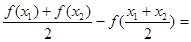 >0,只需要
>0,只需要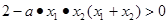 在x1、x2∈(0,1)上恒成立,故可求实数a的取值范围.
在x1、x2∈(0,1)上恒成立,故可求实数a的取值范围.解:(1)
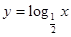 (或其它底在(0,1)上的对数函数)。…………2分
(或其它底在(0,1)上的对数函数)。…………2分(2)函数
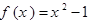 在区间
在区间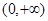 上具有性质L。…………3分
上具有性质L。…………3分证明:任取
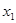 、
、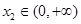 ,且
,且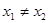
则
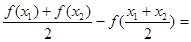
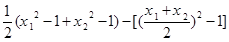
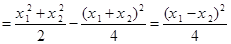

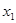 、
、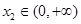 且
且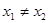 ,
,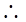
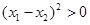 ,
, 即
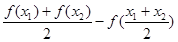 >0,
>0,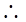
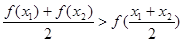
所以函数
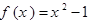 在区间
在区间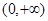 上具有性质L。……………7分
上具有性质L。……………7分(3)任取
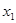 、
、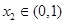 ,且
,且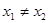
则
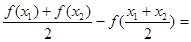
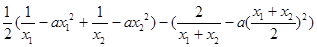
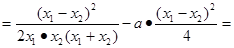
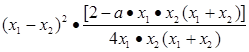

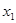 、
、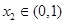 且
且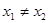 ,
,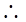
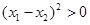 ,
,
要使上式大于零,必须
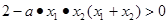 在
在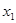 、
、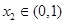 上恒成立,
上恒成立,即
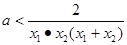 ,
,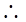
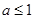 ,即实数
,即实数 的取值范围为
的取值范围为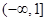 ……………12分
……………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
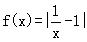
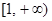 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;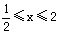 },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系;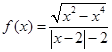 .给出函数
.给出函数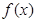 下列性质:⑴
下列性质:⑴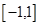 ;⑵
;⑵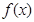 有两零点;⑸
有两零点;⑸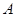 、
、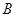 为函数
为函数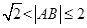 .则函数
.则函数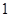
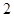
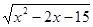 的单调递减区间是 .
的单调递减区间是 .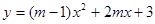 是偶函数,则
是偶函数,则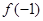 ,
, ,
,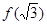 的大小关系为( )
的大小关系为( )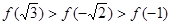
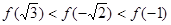
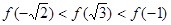
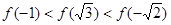
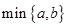 表示
表示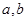 两数中的最小值,若函数
两数中的最小值,若函数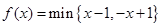 ,则不等式
,则不等式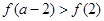 的解集是________________.
的解集是________________. 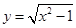
 的单调递减区间为________.
的单调递减区间为________. =
=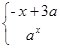
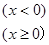
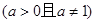 是R上的减函数,则
是R上的减函数,则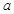 取值范围是( )
取值范围是( )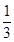 )
)