题目内容
设函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)已知![]() ,若函数
,若函数![]() 的图象总在直线
的图象总在直线![]() 的下方,求
的下方,求![]() 的取值范围;
的取值范围;
(Ⅲ)记![]() 为函数
为函数![]() 的导函数.若
的导函数.若![]() ,试问:在区间
,试问:在区间![]() 上是否存在
上是否存在![]() (
(![]()
![]() )个正数
)个正数![]() …
…![]() ,使得
,使得![]() 成立?请证明你的结论.
成立?请证明你的结论.
解:(Ⅰ)当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以切线的斜率为![]() .…………………………………………2分
.…………………………………………2分
又![]() ,所以切点为
,所以切点为![]() .
.
故所求的切线方程为:![]() 即
即![]() .……………………4分
.……………………4分
(Ⅱ) ,
,![]() ,
,![]() .…………………6分
.…………………6分
令![]() ,则
,则![]() .
.
当 时,
时,![]() ;当
;当 时,
时,![]() .
.
故![]() 为函数
为函数![]() 的唯一极大值点,
的唯一极大值点,
所以![]() 的最大值为
的最大值为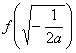 =
=![]() .……………………………8分
.……………………………8分
由题意有![]() ,解得
,解得![]() .
.
所以![]() 的取值范围为
的取值范围为![]() .…………………………………………10分
.…………………………………………10分
(Ⅲ)当![]() 时,
时,![]() . 记
. 记![]() ,其中
,其中![]() .
.
∵当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上为增函数,
上为增函数,
即![]() 在
在![]() 上为增函数.…………………………………………12分
上为增函数.…………………………………………12分
又![]() ,
,
所以,对任意的![]() ,总有
,总有![]() .
.
所以![]() ,
,
又因为![]()
![]() ,所以
,所以![]() .
.
故在区间![]() 上不存在使得
上不存在使得![]() 成立的
成立的![]() (
(![]()
![]() )个正数
)个正数![]() …
…![]() .………………………14分
.………………………14分

练习册系列答案
相关题目
 .
. .
. ,
, 时,求所有使
时,求所有使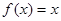 成立的
成立的 的值。
的值。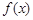 为奇函数,求证:
为奇函数,求证:  ;
; <
< ,且对任意x
,且对任意x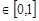 ,
,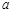 的取值范围.
的取值范围. ,其中
,其中
 判断
判断 在
在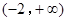 上的单调性.
上的单调性.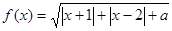 。
。 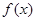 的定义域。
的定义域。