题目内容
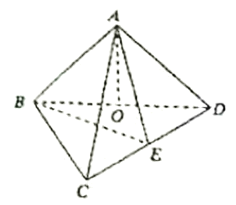
【题目】已知空间四边形ABCD，
，
，
，
，且平面
平面BCD，则该几何体的外接球的表面积为（ ）
A.
B.
C.
D.
【答案】B
【解析】
由题意画出图形，找出外接球的球心，求解三角形得到半径，代入球的表面积公式求解．
如图所示，取BC中点E，连接AE并延长至
的外心G，在中，由
，
，
可得BE＝CE＝3，则BC＝6，又
，
，满足
，则
是为以BD为斜边的直角三角形，
则BD中点F为的外心，∵平面ABC⊥平面BCD，过F作平面BCD的垂线与过G作平面ABC的垂线相交于O，
∴O为空间四边形ABCD的外接球的球心．在中，由正弦定理得
，得AG＝2
．
∴
，则OF＝，∴空间四边形ABCD的外接球的半径R＝OD＝
．
∴空间四边形ABCD的外接球的表面积
．
故选：B．
练习册系列答案
相关题目
