题目内容
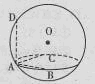
如图,设A,B,C,D为球O上四点,AB,AC,AD两两互相垂直,且AB=AC=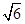 ,AD=2,则A、D两点间的球面距离为
,AD=2,则A、D两点间的球面距离为
A、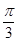 B、
B、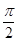 C、
C、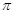 D、
D、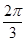
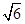 ,AD=2,则A、D两点间的球面距离为
,AD=2,则A、D两点间的球面距离为A、
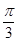 B、
B、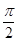 C、
C、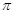 D、
D、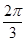

D
构造长方体,利用它们有相同的外接球,求出∠AOB和球的半径即可解答.
解:∵侧棱AB、AC、AD两两垂直
∴以侧棱AB、AC、AD构造长方体,如图,长方体的对角线的中点O即为球的球心,
∵AB=AC=
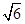 ,AD=2,
,AD=2,∴长方体的对角线2R=4,R=2,
又在三角形AOB中, OA=OD=2,AD=
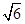
∴∠AOB=π/3
则A、B两点的球面距离为π/3×2=2π/3


练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
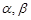 为两个不重合的平面,
为两个不重合的平面,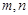 是两条不重合的直线,给出下列四个命题:
是两条不重合的直线,给出下列四个命题: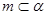 ,
,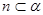 ,
,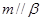 ,
,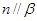 ,则
,则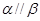 ;②若
;②若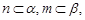
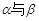 相交且不垂直,则
相交且不垂直,则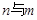 不垂直;③若
不垂直;③若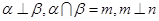 ,则n⊥
,则n⊥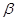 ; ④若
; ④若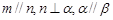 ,则
,则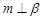 .其中所有真命题的序号是 .
.其中所有真命题的序号是 .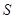 是
是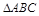 所在平面外的一点,且
所在平面外的一点,且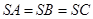 ,若
,若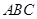 内的射影落在
内的射影落在 ABC外部,则
ABC外部,则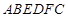 为多面体,平面
为多面体,平面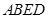 与平面
与平面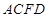 垂直,点
垂直,点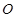 在线段
在线段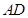 上,
上,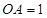 ,
,
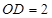 ,△OAB,△OAC,△ODE,△ODF都是正三角形。
,△OAB,△OAC,△ODE,△ODF都是正三角形。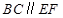 ;
;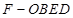 的体积.
的体积.
 直线l , 则由点P和直线l确定的平面的个数是
直线l , 则由点P和直线l确定的平面的个数是  平面ABC,
平面ABC, ,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证:⑴
,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F,求证:⑴ ;⑵
;⑵ .
.
 的两边
的两边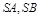 互相垂直,且
互相垂直,且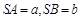 ,则
,则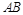 边上的高
边上的高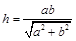 ;现在把结论类比到空间:三棱锥
;现在把结论类比到空间:三棱锥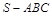 的三条侧棱
的三条侧棱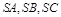 两两相互垂直,
两两相互垂直,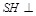 平面
平面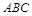 ,且
,且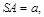
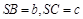 ,则点
,则点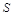 到平面
到平面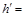
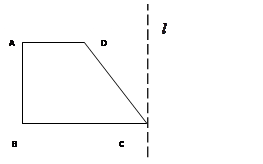
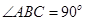 ,AD=a,BC=2a,
,AD=a,BC=2a,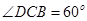 ,在平面ABCD内,过C作
,在平面ABCD内,过C作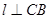 ,以
,以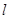 为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积。
为轴将梯形ABCD旋转一周,求所得旋转体的表面积及体积。