题目内容
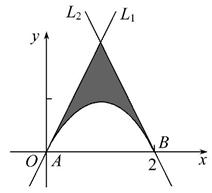
已知抛物线C:y=-x2+2x,过点A(0,0),B(2,0)分别作抛物线的切线L1,L2.
(1)求切线L1和L2的方程.
(2)求抛物线C与切线L1和L2所围成的图形面积S.
解:(1)y'=-2x+2,A(0,0),B(2,0)都在抛物线上,
设切线L1和L2的斜率分别为k1,k2,
则k1=2,k2=-2,故切线L1的方程为y=2x,切线L2的方程为y=-2x+4.
(2)设L1,L2交于点P,
 由
由 得
得
 则P(1,2).
则P(1,2).
S= [2x-(-x2+2x)]dx+
[2x-(-x2+2x)]dx+
 [(-2x+4)-(-x2+2x)]dx
[(-2x+4)-(-x2+2x)]dx
= x2dx+
x2dx+ (x2-4x+4)dx
(x2-4x+4)dx
=
= +
+ =
= .
.
故抛物线C与切线L1和L2所围成的图形面积S为 .
.

练习册系列答案
相关题目
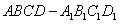 中,侧面
中,侧面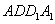 ⊥底面
⊥底面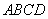 ,
, ,底面
,底面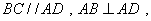
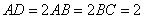 ,O为
,O为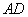 中点。
中点。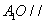 平面
平面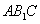 ;
;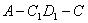 的余弦值.
的余弦值.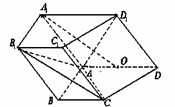
 ,
,  ,若至少存在一个
,若至少存在一个 ,使得
,使得 成立,则实数
成立,则实数 的范围为( )
的范围为( ) B.
B. C.
C. D.
D.
 (B)-1<m<
(B)-1<m< i|的复数z在复平面上对应的点(x,y)的轨迹方程为____________________.
i|的复数z在复平面上对应的点(x,y)的轨迹方程为____________________. -4
-4 D.f(x)=x2+2x
D.f(x)=x2+2x -3x)+1,则f(lg 2)+f
-3x)+1,则f(lg 2)+f =( )
=( ) ,则
,则 的值为________.
的值为________.