题目内容
已知椭圆![]() 的离心率
的离心率![]() ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足![]()
(1)求椭圆C的方程;
(2)是否存在直线![]() ,当直线
,当直线![]() 交椭圆于P、Q两点时,使点F恰为
交椭圆于P、Q两点时,使点F恰为![]() 的垂心. 若存在,求出直线
的垂心. 若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

(1)根据题意得,![]()
![]() ,
, ![]() …………………………2分
…………………………2分
又![]()
![]()
![]()
![]()
![]() 椭圆C的方程为
椭圆C的方程为![]() ……………… 4分
……………… 4分
(2)假设存在直线![]() 满足条件
满足条件
因为![]() ,所以
,所以![]() 设直线PQ 方程为
设直线PQ 方程为![]()
![]() ,由
,由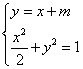 ,消
,消![]()
![]() ,
,
![]()
![]()
![]() …………………………… 8分
…………………………… 8分
又F为![]() 的垂心,
的垂心,
![]()
又![]()
![]()
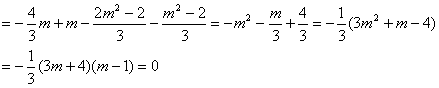
![]() ……………………………………………… 10分
……………………………………………… 10分
经检验均满足![]() ……………………………………………… 11分
……………………………………………… 11分
![]() 存在满足条件直线
存在满足条件直线![]() 方程为:
方程为:
![]() ………………………………… 12分
………………………………… 12分

练习册系列答案
相关题目
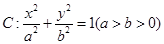 的离心率
的离心率 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足 (1)求椭圆C的方程;
(1)求椭圆C的方程;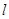 ,当直线
,当直线 的垂心(三角形三条高的交点)?若存在,求出直线
的垂心(三角形三条高的交点)?若存在,求出直线
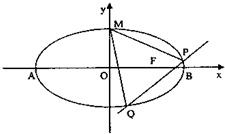 已知椭圆
已知椭圆 的离心率
的离心率 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足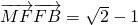 .
.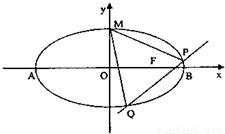 已知椭圆
已知椭圆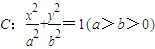 的离心率
的离心率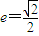 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足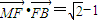 .
.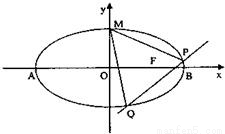 已知椭圆
已知椭圆 的离心率
的离心率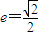 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足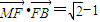 .
.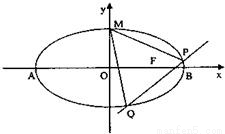 已知椭圆
已知椭圆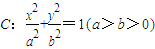 的离心率
的离心率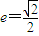 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足 .
.