题目内容
已知椭圆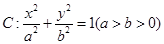 的离心率
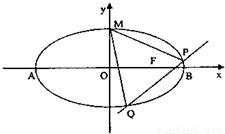
的离心率 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足 (1)求椭圆C的方程;
(1)求椭圆C的方程;
(2)是否存在直线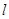 ,当直线
,当直线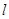 交椭圆于P、Q两点时,使点F恰为
交椭圆于P、Q两点时,使点F恰为 的垂心(三角形三条高的交点)?若存在,求出直线
的垂心(三角形三条高的交点)?若存在,求出直线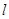 方程;若不存在,请说明理由。
方程;若不存在,请说明理由。

【答案】
(1)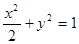 ;(2)当
;(2)当 时,△
时,△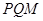 不存在,故舍去
不存在,故舍去 .
.
当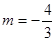 时,所求直线
时,所求直线 存在,且直线
存在,且直线 的方程为
的方程为 .
.
【解析】第一问中利用根据题意得,
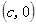 ,
, ,
, ,
,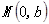

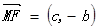 ,
,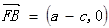 ,
,
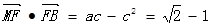 ,又
,又 ,
,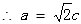
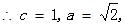
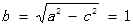
第二问中,假设存在直线 交椭圆于
交椭圆于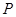 ,
, 两点,且
两点,且 为△
为△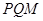 的垂心,
的垂心,
设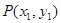 ,
,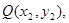
因为 ,
, ,故
,故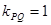 .
…………7分
.
…………7分
于是设直线 的方程为
的方程为 ,
,
由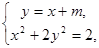 得
得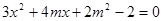 ,结合韦达定理并由题意应有
,结合韦达定理并由题意应有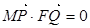 ,又
,又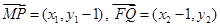 ,得到结论。
,得到结论。
解:根据题意得,
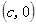 ,
, ,
, ,
,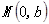

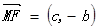 ,
,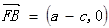 ,
,
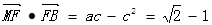 ,又
,又 ,
,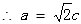
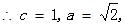
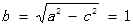
故椭圆方程为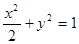 .
…………5分
.
…………5分
(Ⅱ)假设存在直线 交椭圆于
交椭圆于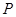 ,
, 两点,且
两点,且 为△
为△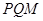 的垂心,
的垂心,
设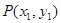 ,
,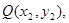
因为 ,
, ,故
,故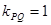 . …………7分
. …………7分
于是设直线 的方程为
的方程为 ,
,
由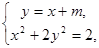 得
得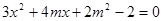 .
.
由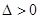 ,得
,得 ,
且
,
且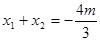 ,
,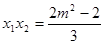 . ……9分
. ……9分
由题意应有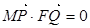 ,又
,又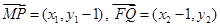 ,
,
故 ,
,
得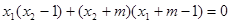 .
.
即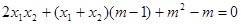 .
.
整理得 .
.
解得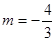 或
或 .
…………11分
.
…………11分
经检验,当 时,△
时,△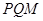 不存在,故舍去
不存在,故舍去 .
.
当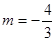 时,所求直线
时,所求直线 存在,且直线
存在,且直线 的方程为
的方程为 .
.
…………12分

练习册系列答案
相关题目
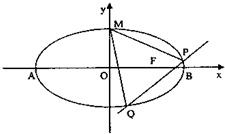 已知椭圆
已知椭圆 的离心率
的离心率 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足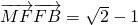 .
. 已知椭圆
已知椭圆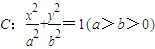 的离心率
的离心率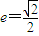 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足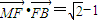 .
.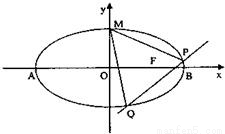 已知椭圆
已知椭圆 的离心率
的离心率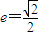 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足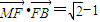 .
.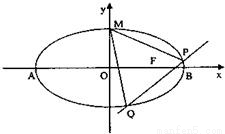 已知椭圆
已知椭圆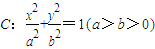 的离心率
的离心率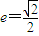 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足 .
.