题目内容
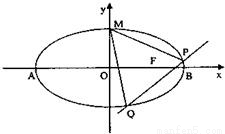 已知椭圆
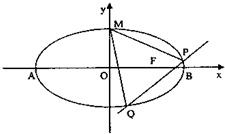
已知椭圆 的离心率
的离心率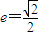 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足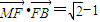 .
.(1)求椭圆C的方程;
(2)是否存在直线l,当直线l交椭圆于P、Q两点时,使点F恰为△PQM的垂心.若存在,求出直线l的方程;若不存在,请说明理由.
【答案】分析:(1)根据题意得,F(c,0),A(-a,0),B(a,0),M(0,b), ,从而导出c2=1,a2=2,b2=1,由此可知椭圆C的方程.
,从而导出c2=1,a2=2,b2=1,由此可知椭圆C的方程.
(2)假设存在直线l满足条件,使F是三角形MPQ的垂心.设PQ直线y=x+m,P(x1,y1),Q(x2,y2), ,3x2+4mx+2m2-2=0,再由根的判别式和根与系数的关系进行求解.
,3x2+4mx+2m2-2=0,再由根的判别式和根与系数的关系进行求解.
解答:解:(1)根据题意得,F(c,0),A(-a,0),B(a,0),M(0,b)
∴
∴ (2分)
(2分)
又
∴
∴
∴c2=1,a2=2,b2=1
∴椭圆C的方程为 .(4分)
.(4分)
(2)假设存在直线l满足条件,使F是三角形MPQ的垂心.
因为KMF=-1,且FM⊥l,
所以k1=1,
所以设PQ直线y=x+m,
且设P(x1,y1),Q(x2),y2
由
消y,得3x2+4mx+2m2-2=0
△=16m2-12(2m2-2)>0,m2<3 .
.
y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2= .(8分)
.(8分)
又F为△MPQ的垂心,
∴PF⊥MQ,∴
又
∴ =
= ∴
∴ ,
,
∴ (10分)
(10分)
经检验满足m2<3(11分)
∴存在满足条件直线l方程为:x-y+1=0,3x-3y-4=0(12分)
∵x-y+1=0过M点 即MP重合 不构成三角形,
∴3x-3y-4=0满足题意.
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意公式的灵活运用.
 ,从而导出c2=1,a2=2,b2=1,由此可知椭圆C的方程.
,从而导出c2=1,a2=2,b2=1,由此可知椭圆C的方程.(2)假设存在直线l满足条件,使F是三角形MPQ的垂心.设PQ直线y=x+m,P(x1,y1),Q(x2,y2),
 ,3x2+4mx+2m2-2=0,再由根的判别式和根与系数的关系进行求解.
,3x2+4mx+2m2-2=0,再由根的判别式和根与系数的关系进行求解.解答:解:(1)根据题意得,F(c,0),A(-a,0),B(a,0),M(0,b)
∴

∴
 (2分)
(2分)又

∴

∴

∴c2=1,a2=2,b2=1
∴椭圆C的方程为
 .(4分)
.(4分)(2)假设存在直线l满足条件,使F是三角形MPQ的垂心.
因为KMF=-1,且FM⊥l,
所以k1=1,
所以设PQ直线y=x+m,
且设P(x1,y1),Q(x2),y2
由

消y,得3x2+4mx+2m2-2=0
△=16m2-12(2m2-2)>0,m2<3
 .
.y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2=
 .(8分)
.(8分)又F为△MPQ的垂心,
∴PF⊥MQ,∴

又

∴
 =
= ∴
∴ ,
,∴
 (10分)
(10分)经检验满足m2<3(11分)
∴存在满足条件直线l方程为:x-y+1=0,3x-3y-4=0(12分)
∵x-y+1=0过M点 即MP重合 不构成三角形,
∴3x-3y-4=0满足题意.
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
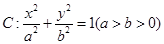 的离心率
的离心率 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足 (1)求椭圆C的方程;
(1)求椭圆C的方程; ,当直线
,当直线 的垂心(三角形三条高的交点)?若存在,求出直线
的垂心(三角形三条高的交点)?若存在,求出直线
 已知椭圆
已知椭圆 的离心率
的离心率 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足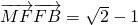 .
.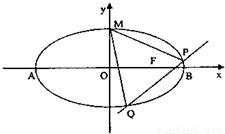 已知椭圆
已知椭圆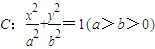 的离心率
的离心率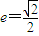 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足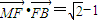 .
.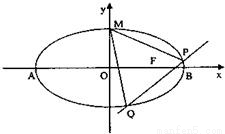 已知椭圆
已知椭圆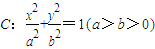 的离心率
的离心率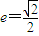 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足 .
.