题目内容
设点P为直线y=
x与椭圆
+
=1(a>b>c>0)在第一象限内的交点,点F是椭圆的右焦点,若PF垂直于x轴,则椭圆的离心率e=
.
| b |
| 2a |
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 5 |
2
| ||
| 5 |
分析:先求出P的坐标,代入椭圆方程,即可求得离心率.
解答:解:设椭圆的右焦点F(c,0),代入直线y=
x,可得y=
∴P(c,
)
代入
+
=1可得
+
=1
∴
=
∴e=
故答案为:
| b |
| 2a |
| bc |
| 2a |
∴P(c,
| bc |
| 2a |
代入
| x2 |
| a2 |
| y2 |
| b2 |
| c2 |
| a2 |
| ||
| b2 |
∴
| c2 |
| a2 |
| 4 |
| 5 |
∴e=
2
| ||
| 5 |
故答案为:
2
| ||
| 5 |
点评:本题考查椭圆的离心率,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 给定椭圆C:
给定椭圆C: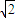 ,并记点P的轨迹为曲线C.
,并记点P的轨迹为曲线C.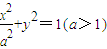 短轴的两个端点,F为椭圆的一个焦点,△B1FB2为正三角形,
短轴的两个端点,F为椭圆的一个焦点,△B1FB2为正三角形,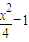 上,C2在点P处的切线与椭圆C1交于A、C两点,若点P是线段AC的中点,求AC的直线方程.
上,C2在点P处的切线与椭圆C1交于A、C两点,若点P是线段AC的中点,求AC的直线方程.