题目内容
12．若正方形ABCD的边长为3，$\overrightarrow{DE}$=2$\overrightarrow{EC}$，$\overrightarrow{BF}$=2$\overrightarrow{FC}$，则$\overrightarrow{BE}$•$\overrightarrow{DF}$=-6．分析 将所求利用正方形的各边表示，展开整理可得．
解答 解：因为正方形ABCD的边长为3，$\overrightarrow{DE}$=2$\overrightarrow{EC}$，$\overrightarrow{BF}$=2$\overrightarrow{FC}$，所以$\overrightarrow{BE}$•$\overrightarrow{DF}$=（$\overrightarrow{BC}+\overrightarrow{CE}$）•（$\overrightarrow{DC}+\overrightarrow{CF}$）=$\overrightarrow{BC}•\overrightarrow{DC}+\overrightarrow{BC}•\overrightarrow{CF}$+$\overrightarrow{CE}•\overrightarrow{DC}+\overrightarrow{CE}•\overrightarrow{CF}$=0-3-3+0=-6；
故答案为：-6．
点评 本题考查了平面向量的三角形法则的运用以及数量积公式的运用；关键是将所求用正方形的各边对应的向量表示．
练习册系列答案
相关题目
2．一个几何体的三视图如图所示，则其体积为（ ）
| A． | $\frac{4}{3}$（π+1） | B． | $\frac{2}{3}$（π+1） | C． | $\frac{4}{3}$（π+$\frac{1}{2}$） | D． | $\frac{2}{3}$（π+$\frac{1}{2}$） |
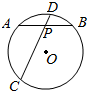如图，在半径为$\sqrt{7}$的⊙O中，弦AB、CD相交于点P，PA=PB=2，PD=1．
函数f（x）=Asin（ωx+φ）（A，ω，φ为常数，A＞0，ω＞0，0＜φ＜π）的图象如图所示，则A=2，ω=2，F（$\frac{π}{3}$）=1．