题目内容
4.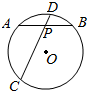 如图,在半径为$\sqrt{7}$的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1.
如图,在半径为$\sqrt{7}$的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1.(1)求证相交弦定理:AP•PB=PD•PC;
(2)求圆心O到弦CD的距离.
分析 (1)证明△APC∽△DPB,可得AP•PB=PD•PC;
(2)利用垂径定理、勾股定理,即可求圆心O到弦CD的距离.
解答 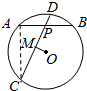 (1)证明:连接AC,DB,则有∠ACP=∠ABD,∠APC=∠DPB,
(1)证明:连接AC,DB,则有∠ACP=∠ABD,∠APC=∠DPB,
∴△APC∽△DPB,
∴$\frac{AP}{PD}=\frac{PC}{PB}$,
∴AP•PB=PD•PC;
(2)解:由(1)知,AP•PB=PD•PC,可得2×2=1×PC,
∴PC=4,
过O作OM⊥CD于点M,由圆的性质可知CM=2.5,
在△OMC中,d=$\sqrt{7-2.{5}^{2}}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查三角形相似的判定与性质,考查垂径定理、勾股定理,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
15.已知a,b是实数,则“a>|b|”是“a2>b2”的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
16.在等差数列{an}中,a9=$\frac{1}{2}$a12+6,则该数列的前11项和为( )
| A. | 12 | B. | 72 | C. | 132 | D. | 192 |
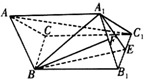 如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°.
如图,斜三棱柱ABC-A1B1C1中,A1B1=A1C1,点E,F分别是B1C1,A1B1的中点,AA1=AB=BE=1,∠A1AB=60°. 一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298.
一个由若干行数字组成的数表,从第二行起,每一行中的数字均等于其肩上两个数字之和,最后一行仅有一个数,第一行是前100个正整数按从小到大排成的行,则最后一行的数是101×298. 如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,
如图,四边形ABCD为平行四边形,AB=5,AD=4,BD=3,将△BCD沿着BD翻折到平面BC1D处(不与平面ABCD重合),E,F分别为对边AB,C1D的中点,