题目内容
已知圆心为C的圆经过点(1,1)和(2,-2),且圆心C在直线l:x-y+1=0上.
(1)求圆心为C的圆的标准方程;
(2)已知点A是圆心为C的圆上动点,B(2,1),求|AB|的取值范围.
(1)求圆心为C的圆的标准方程;
(2)已知点A是圆心为C的圆上动点,B(2,1),求|AB|的取值范围.
(1)设圆心C(a,a+1),则
∵圆经过点(1,1)和(2,-2),
∴(a-1)2+a2=(a-2)2+(a-3)2=r2,
∴a=-3,r=5,
∴圆的标准方程为(x+3)2+(y+2)2=25;
(2)设A(-3+5cosα,-2+5sinα),则
∵B(2,1),
∴|AB|=
=
,
∴|AB|的取值范围为[
,
,即[
-5,
+5].
∵圆经过点(1,1)和(2,-2),
∴(a-1)2+a2=(a-2)2+(a-3)2=r2,
∴a=-3,r=5,
∴圆的标准方程为(x+3)2+(y+2)2=25;
(2)设A(-3+5cosα,-2+5sinα),则
∵B(2,1),
∴|AB|=
| (5+5cosα)2+(3+5sinα)2 |
59+10
|
∴|AB|的取值范围为[
59-10
|
59+10
|
| 34 |
| 34 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
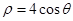 ,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是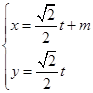 (t是参数).
(t是参数).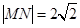 ,求实数m的值.
,求实数m的值.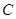 上的动点
上的动点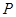 是坐标为
是坐标为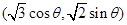 .
.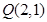 作曲线
作曲线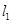 、
、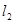 ,证明
,证明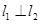 .
.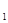 :
: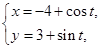 (t为参数), C
(t为参数), C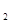 :
: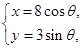 (
(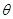 为参数)。
为参数)。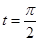 ,Q为C
,Q为C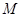 中点
中点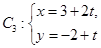 (t为参数)距离的最小值。
(t为参数)距离的最小值。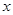 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线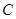 的极坐标方程为
的极坐标方程为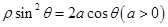 ,过点
,过点 的直线
的直线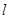 的参数方程为
的参数方程为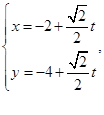 (
(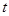 为参数),直线
为参数),直线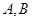 两点.
两点.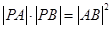 ,求
,求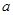 的值.
的值. 和直线
和直线 ,
, 的直角坐标方程;
的直角坐标方程; 时,求直线
时,求直线