题目内容
已知:椭圆 (a>b>0)过(0,1)点,离心率
(a>b>0)过(0,1)点,离心率 ;直线l:y=kx+m(m>0)与圆O:x2+y2=1相切,并与椭圆C交于不同的两点A、B,(O为坐标原点).
;直线l:y=kx+m(m>0)与圆O:x2+y2=1相切,并与椭圆C交于不同的两点A、B,(O为坐标原点).
Ⅰ.求椭圆C的方程及m与k的关系式m=f(k);
Ⅱ.设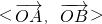 =θ,且满足
=θ,且满足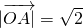 ,
,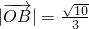 ,
,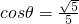 求直线l的方程;
求直线l的方程;
Ⅲ.在Ⅱ.的条件下,求三角形AOB的面积.
解:Ⅰ.∵椭圆 ,过(0,1)点,∴b=1,
,过(0,1)点,∴b=1,
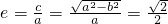 ∴a2=2,
∴a2=2,
∴椭圆C方程为: ;
;
∵直线l:y=kx+m(m>0)与圆x2+y2=1相切,
∴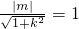 ,
,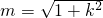 ,即
,即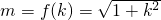 ;
;
Ⅱ. 消去y得(2k2+1)x2+4kmx+2m2-2=0,
消去y得(2k2+1)x2+4kmx+2m2-2=0,
△=8k2>0,∴k≠0
设A(x1,y1),B(x2,y2),则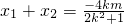 ,
, ,
, =|
=| |•|
|•| |•cosθ=
|•cosθ= •
• •
• =
= ;
;
又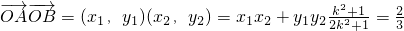
k2=1,k=±1;∴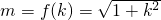 =
= ,
,
直线l的方程为: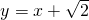 或
或 ,
,
Ⅲ.由Ⅱ.知k=±1;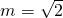 消去y得
消去y得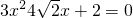 ,
,
 ,
,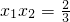 由弦长公式:
由弦长公式: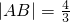 ,
,
∴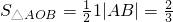 ,
,
∵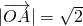 ∴
∴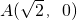
∴直线AB过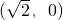 点;
点;
∵< >=θ,
>=θ,
且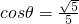 ∴
∴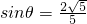 ,kOB=tanθ=±2
,kOB=tanθ=±2
∴lOB:y=±2x,与
联立解得: ,
,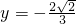 或
或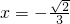 ,
,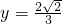
即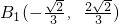 ,
,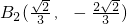 ,
,
由两点得AB的方程为: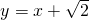 ,
,
由前面解知:|OA|为三角形的底边,|yB|为三角形的高,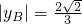 ,S△AOB=
,S△AOB= |
| |•|yB|=
|•|yB|= ×
× ×
× =
= .
.
分析:Ⅰ.由题意可知b=1,a2=2,由此可以求出椭圆C的方程.再由直线l:y=kx+m(m>0)与圆x2+y2=1相切,能够导出m与k的关系式m=f(k).
Ⅱ.由 消去y得(2k2+1)x2+4kmx+2m2-2=0,然后由根的判别式和根与系数的关系求直线l的方程.
消去y得(2k2+1)x2+4kmx+2m2-2=0,然后由根的判别式和根与系数的关系求直线l的方程.
Ⅲ.|OA|为三角形的底边,|yB|为三角形的高,由此能够推导出三角形AOB的面积.
点评:本题考查椭圆知识的综合运用,有一定的难度,在解题时要认真审题,注意公式的灵活运用.
 ,过(0,1)点,∴b=1,
,过(0,1)点,∴b=1,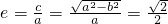 ∴a2=2,
∴a2=2,∴椭圆C方程为:
 ;
;∵直线l:y=kx+m(m>0)与圆x2+y2=1相切,
∴
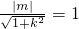 ,
,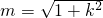 ,即
,即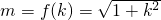 ;
;Ⅱ.
 消去y得(2k2+1)x2+4kmx+2m2-2=0,
消去y得(2k2+1)x2+4kmx+2m2-2=0,△=8k2>0,∴k≠0
设A(x1,y1),B(x2,y2),则
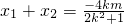 ,
, ,
, =|
=| |•|
|•| |•cosθ=
|•cosθ= •
• •
• =
= ;
;又
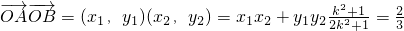
k2=1,k=±1;∴
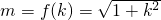 =
= ,
,直线l的方程为:
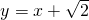 或
或 ,
,Ⅲ.由Ⅱ.知k=±1;
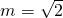 消去y得
消去y得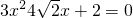 ,
, ,
,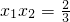 由弦长公式:
由弦长公式: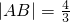 ,
,∴
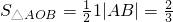 ,
,∵
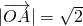 ∴
∴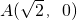
∴直线AB过
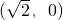 点;
点;∵<
 >=θ,
>=θ,且
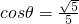 ∴
∴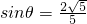 ,kOB=tanθ=±2
,kOB=tanθ=±2∴lOB:y=±2x,与

联立解得:
 ,
,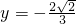 或
或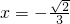 ,
,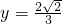
即
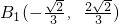 ,
,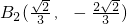 ,
,由两点得AB的方程为:
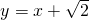 ,
,由前面解知:|OA|为三角形的底边,|yB|为三角形的高,
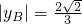 ,S△AOB=
,S△AOB= |
| |•|yB|=
|•|yB|= ×
× ×
× =
= .
.分析:Ⅰ.由题意可知b=1,a2=2,由此可以求出椭圆C的方程.再由直线l:y=kx+m(m>0)与圆x2+y2=1相切,能够导出m与k的关系式m=f(k).
Ⅱ.由
 消去y得(2k2+1)x2+4kmx+2m2-2=0,然后由根的判别式和根与系数的关系求直线l的方程.
消去y得(2k2+1)x2+4kmx+2m2-2=0,然后由根的判别式和根与系数的关系求直线l的方程.Ⅲ.|OA|为三角形的底边,|yB|为三角形的高,由此能够推导出三角形AOB的面积.
点评:本题考查椭圆知识的综合运用,有一定的难度,在解题时要认真审题,注意公式的灵活运用.

练习册系列答案
相关题目
 (a>b>0),过点A(-a,0),B(0,b)的直线倾斜角为
(a>b>0),过点A(-a,0),B(0,b)的直线倾斜角为 ,原点到该直线的距离为
,原点到该直线的距离为 .
. ,求直线EF的方程;
,求直线EF的方程;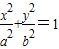 (a>b>0),过点
(a>b>0),过点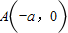 ,
,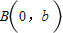 的直线倾斜角为
的直线倾斜角为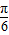 ,原点到该直线的距离为
,原点到该直线的距离为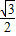 .
.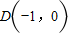 与椭圆交于E,F两点,若
与椭圆交于E,F两点,若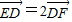 ,求直线EF的方程.
,求直线EF的方程.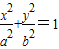 (a>b>0),过点
(a>b>0),过点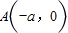 ,
,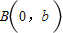 的直线倾斜角为
的直线倾斜角为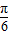 ,原点到该直线的距离为
,原点到该直线的距离为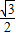 .
.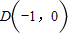 与椭圆交于E,F两点,若
与椭圆交于E,F两点,若 ,求直线EF的方程.
,求直线EF的方程.