题目内容
如图1,在直角梯形 中,
中, ,
, ,
, .将
.将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.

(1) 求证: 平面
平面 ;(2) 求几何体
;(2) 求几何体 的体积.
的体积.
【答案】
(1)见解析 (2) 
【解析】(1)证明: 即可.
即可.
(2)因为平面
 平面
平面 ,并且AD=DC,取AC的中点M,连接DM,则
,并且AD=DC,取AC的中点M,连接DM,则 ,所以DM就是三棱锥
,所以DM就是三棱锥 的高,从而易求其体积.
的高,从而易求其体积.
解:(Ⅰ)在图1中,可得 ,从而
,从而 ,故
,故
取 中点
中点 连结
连结 ,则
,则 ,又面
,又面
 面
面 ,
,
面
 面
面
 ,
, 面
面 ,从而
,从而 平面
平面 ,……4分
,……4分
∴
又 ,
, ,
,
∴ 平面
平面 ……8分
……8分
另解:在图1中,可得 ,从而
,从而 ,故
,故
∵面ACD 面
面 ,面ACD
,面ACD 面
面
 ,
, 面
面 ,从而
,从而 平面
平面
(Ⅱ) 由(Ⅰ)可知 为三棱锥
为三棱锥 的高.
的高.  ,
, ……11分
……11分
所以 ……13分
……13分
由等积性可知几何体 的体积为
的体积为 ……14分
……14分

练习册系列答案
相关题目


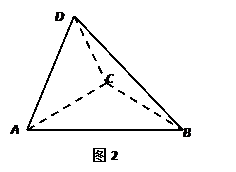

 中,
中, ,
, ,
, ,
,  为线段
为线段 的中点.将
的中点.将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
 平面
平面 ;
; 的余弦值.
的余弦值.