题目内容
(本题满分12分)如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,
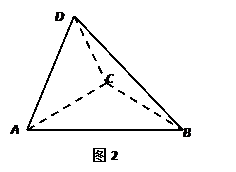

![]() .将
.将![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到几何体
,得到几何体![]() ,如图2所示.(Ⅰ) 求证:
,如图2所示.(Ⅰ) 求证:![]() 平面
平面![]() ;(Ⅱ) 求几何体
;(Ⅱ) 求几何体![]() 的体积.
的体积.
![]()
(Ⅰ) 略 (Ⅱ) ![]()
解析:
:(Ⅰ)在图1中,可得![]() ,从而
,从而![]() ,故
,故![]()
取![]() 中点
中点![]() 连结
连结![]() ,则
,则![]() ,又面
,又面![]()
![]() 面
面![]() ,
,
面![]()
![]() 面
面![]()
![]() ,
,![]() 面
面![]() ,从而
,从而![]() 平面
平面![]() , ……4分
, ……4分
∴![]() 又
又![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ……6分
……6分
另解:在图1中,可得![]() ,从而
,从而![]() ,故
,故![]()
∵面![]()
![]() 面
面![]() ,面
,面![]()
![]() 面
面![]()
![]() ,
,![]() 面
面![]() ,从而
,从而![]() 平面
平面![]()
(Ⅱ) 由(Ⅰ)可知![]() 为三棱锥
为三棱锥![]() 的高.
的高. ![]() ,
,![]() ……9分
……9分
所以![]() …11分
…11分
由等积性可知几何体![]() 的体积为
的体积为![]() ……12分
……12分

练习册系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
