题目内容
如图AB是半圆⊙O的直径，点C为半圆圆周上一点，OD⊥AC交圆周于点D，交AC于点E，且AB=4，∠BAC=30°，则CD=2
2
．分析：连接OC，由圆心角定理可得
的度数，进而得到
的度数，由OD⊥AC结合垂径定理，可得OD平分
，进而得到
及其所对圆心角∠DOC的度数，判断出△OCD的形状，结合直径为4，可得答案．
 |
| BC |
|
| AC |
|
| AC |
|
| DC |
解答：
解：连接OC，
∵∠BAC=30°
∴
的度数为60°，
的度数为120°
∵OD⊥AC
∴OD平分
，即
的度数为60°，
∴∠DOC=60°，
又∵OC=OD
∴△OCD为正三角形
又∵AB=4，
∴CD=2
故答案为：2
解：连接OC，∵∠BAC=30°
∴
|
| BC |
|
| AC |
∵OD⊥AC
∴OD平分
|
| AC |
|
| DC |
∴∠DOC=60°，
又∵OC=OD
∴△OCD为正三角形
又∵AB=4，
∴CD=2
故答案为：2
点评：本题考查的知识点是与圆相关的比例线段，其中根据垂径定理，求出
及其所对圆心角∠DOC的度数，进而判断出△OCD的形状，是解答的关键．
|
| DC |
练习册系列答案
相关题目
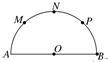如图，已知AB是半圆O的直径，AB=8，M、N、P是将半圆圆周四等分的三个分点
的取值范围是
=____________.