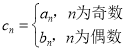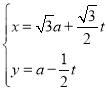题目内容
【题目】已知椭圆C：
（
）经过点
，离心率为
，
，
分别为椭圆的左、右焦点.
（1）求椭圆C的标准方程；
（2）若点
（
）在椭圆C上，求证；直线
与直线
关于直线l：
对称.
【答案】（1）
（2）见解析
【解析】
（1）将点
代入椭圆方程，由离心率得到
关系，结合
，即可求解；
（2）若
，根据椭圆的对称性即可得证，若
，只需证明
关于直线l的对称点
在直线
上，根据点关于直线对称关系求出点坐标，而后证明
三点共线，即可证明结论.
（1）解：由题意知
可得
，
，
所以椭圆C的标准方程为.
（2）证明：若，则
，
此时直线与直线
关于直线l对称.
设关于直线l的对称点为
，
若，则
则
，
，
要证直线与直线关于直线l对称，只需证Q，P，
三点共线，
即证
，即证
，
因为
，
综上，直线与直线关于直线l对称.
尖子生新课堂课时作业系列答案
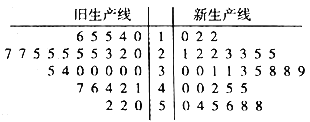
英才计划同步课时高效训练系列答案
【题目】近几年，我国鲜切花产业得到了快速发展，相关部门制定了鲜切花产品行业等级标准，统一使用综合指标值
进行衡量，如下表所示.某花卉生产基地准备购进一套新型的生产线，现进行设备试用，分别从新旧两条生产线加工的产品中选取30个样品进行等级评定，整理成如图所示的茎叶图.
综合指标 |
|
|
|
质量等级 | 三级 | 二级 | 一级 |
（Ⅰ）根据茎叶图比较两条生产线加工的产品的综合指标值的平均值及分散程度（直接给出结论即可）；
（Ⅱ）若从等级为三级的样品中随机选取3个进行生产流程调查，其中来自新型生产线的样品个数为
，求的分布列；
（Ⅲ）根据该花卉生产基地的生产记录，原有生产线加工的产品的单件平均利润为4元，产品的销售率（某等级产品的销量与产量的比值）及产品售价如下表：
三级花 | 二级花 | 一级花 | |
销售率 |
|
|
|
单件售价 | 12元 | 16元 | 20元 |
预计该新型生产线加工的鲜切花单件产品的成本为10元，日产量3000件.因为鲜切花产品的保鲜特点，未售出的产品统一按原售价的50%全部处理完.如果仅从单件产品利润的角度考虑，该生产基地是否需要引进该新型生产线？
【题目】为实现国民经济新“三步走”的发展战略目标，国家加大了扶贫攻坚的力度．某地区在2015 年以前的年均脱贫率（脱离贫困的户数占当年贫困户总数的比）为
．2015年开始，全面实施“精准扶贫”政策后，扶贫效果明显提高，其中2019年度实施的扶贫项目，各项目参加户数占比（参加该项目户数占 2019 年贫困户总数的比）及该项目的脱贫率见下表：
实施项目 | 种植业 | 养殖业 | 工厂就业 | 服务业 |
参加用户比 |
|
|
|
|
脱贫率 |
|
|
|
|
那么
年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的（ ）
A.
倍B.
倍C.
倍D.
倍
