题目内容
1.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE:EB=AF:FD=1:4,又H,G分别是BC,CD的中点,则( )| A. | BD∥平面EFG,且四边形EFGH是平行四边形 | |
| B. | EF∥平面BCD,且四边形EFGH是梯形 | |
| C. | HG∥平面ABD,且四边形EFGH是平行四边形 | |
| D. | EH∥平面ADC,且四边形EFGH是梯形 |
分析 画出图形,根据条件便可得到EF∥HG,且EF≠HG,从而说明四边形EFGH为梯形,而由条件知EF∥BD,从而根据线面平行的判定定理即可得出EF∥平面BCD,这样便可找出正确选项.
解答 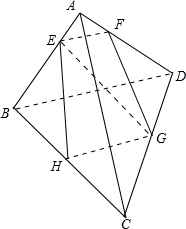 解:如图,
解:如图,
由条件知,EF∥BD,$EF=\frac{1}{5}BD$,GH∥BD,且$HG=\frac{1}{2}BD$;
∴EF∥HG,且$EF=\frac{2}{5}HG$;
∴四边形EFGH为梯形;
EF∥BD,EF?平面BCD,BD?平面BCD;
∴EF∥平面BCD;
若EH∥平面ADC,则EH∥FG,显然EH不平行FG;
∴EH不平行平面ADC;
∴选项B正确.
故选:B.
点评 考查平行线分线段成比例定理,中位线的性质,以及相似三角形对应边的比例关系,梯形的定义,线面平行的判定定理及性质定理.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
12.已知f(x)=x(2014-lnx),若f′(x0)=2013,则x0=( )
| A. | 1 | B. | ln2 | C. | $\frac{1}{e}$ | D. | e |
16.设A,B,C,D是空间中的四个不同的点,则下列说法错误的是( )
| A. | 若AC与BD共面,则AD与BC也共面 | |
| B. | 若AC与BD是异面直线,则AD与BC也是异面直线 | |
| C. | 若AC与BD是相交直线,则AD与BC也是相交直线 | |
| D. | 若A,B,C,D不共面,则AC与BD既不平行也不相交 |
 如图,函数y=cosx+|x|的图象经过矩形ABCD的顶点C,D.若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于0.5.
如图,函数y=cosx+|x|的图象经过矩形ABCD的顶点C,D.若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于0.5.