题目内容
【题目】如图，点P、Q、R、S分别在正方体的四条棱上，并且是所在棱的中点，则直线PQ与RS是异面直线的一个图是（ ）
A.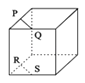
B.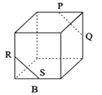
C.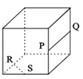
D.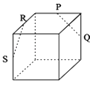
【答案】C
【解析】解：A 中的PQ与RS是两条平行且相等的线段，故选项A不满足条件．
B 中的PQ与RS是两条平行且相等的线段，故选项B也不满足条件．
D 中，由于PR平行且等于
SQ，故四边形SRPQ为梯形，
故PQ与RS是两条相交直线，它们和棱交与同一个点，故选项D不满足条件．
C 中的PQ与RS是两条既不平行，又不相交的直线，故选项C满足条件．
故选 C
【考点精析】利用异面直线的判定对题目进行判断即可得到答案，需要熟知过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.（不在任何一个平面内的两条直线）．
练习册系列答案
相关题目
