题目内容
14．已知直线l过点P（-2，-2），且与以A（-1，1），B（3，0）为端点的线段AB相交，则直线l的斜率的取值范围是[$\frac{5}{2}$，3]．分析 先根据A，B，P的坐标分别求得直线AP和BP的斜率，结合图象，最后综合可得答案．
解答 
解：直线AP的斜率K=$\frac{1+2}{-1+2}$=3，
直线BP的斜率K′=$\frac{3+2}{0+2}$=$\frac{5}{2}$
由图象可知，则直线l的斜率的取值范围是[$\frac{5}{2}$，3]，
故答案为：[$\frac{5}{2}$，3]，
点评 本题给出经过定点P的直线l与线段AB有公共点，求l的斜率取值范围．着重考查了直线的斜率与倾斜角及其应用的知识，属于中档题．
练习册系列答案
快捷英语周周练系列答案
相关题目
4．已知椭圆的一个焦点与抛物线y2=4x的焦点重合，且椭圆的离心率为$\frac{\sqrt{2}}{2}$，该椭圆的方程为（ ）
| A． | $\frac{{x}^{2}}{2}+{y}^{2}=1$ | B． | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$ | C． | $\frac{{y}^{2}}{2}+{x}^{2}=1$ | D． | $\frac{{y}^{2}}{4}+\frac{{x}^{2}}{2}=1$ |
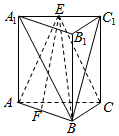如图，在三棱柱ABC-A1B1C1中，侧棱垂直于底面，AB⊥BC，$A{A_1}=AC=2，AB=\sqrt{3}$，E，F分别是A1C1，AB的中点．
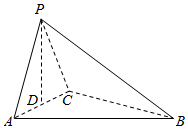如图所示，在三棱锥P-ABC中，点P在平面ABC上的射影D与AC的中点重合，已知BC=2AC=8，AB=4$\sqrt{5}$．