题目内容
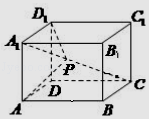
【题目】体积为 ![]() 的球有一个内接正三棱锥P﹣ABC,PQ是球的直径,∠APQ=60°,则三棱锥P﹣ABC的体积为( )
的球有一个内接正三棱锥P﹣ABC,PQ是球的直径,∠APQ=60°,则三棱锥P﹣ABC的体积为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:由题意可得球O的半径为2,如图, 因为PQ是球的直径,所以∠PAQ=90°,∠APQ=60°,可得AP=2,
△ABC所在小圆圆心为O′,可由射影定理AP2=PO′PQ,所以PO′=1,AO′= ![]() ,
,
因为O′为△ABC的中心,所以可求出△ABC的边长为3,面积为 ![]() ,
,
因此,三棱锥P﹣ABC的体积为V= ![]() =
= ![]() .
.
故选:C.
【考点精析】本题主要考查了球内接多面体的相关知识点,需要掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长才能正确解答此题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目