题目内容
(本小题12分)设有数列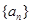 ,
,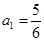 ,若以
,若以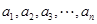 为系数的二次方程
为系数的二次方程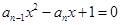 都有根
都有根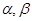 ,且满足
,且满足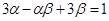 。
。
(1)求证:数列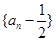 是等比数列。
是等比数列。
(2)求数列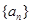 的通项
的通项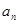 以及前n项和
以及前n项和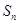 。
。
【答案】
(1)见解析;
(2)
 。
。
【解析】
试题分析:解:(1) ,
,  代入
代入 得
得


 数列
数列 是等比数列。
5分
是等比数列。
5分
(2)因为数列 是公比为
是公比为 的等比数列,且其首项为
的等比数列,且其首项为
所以
即 。
8分
。
8分

 12分
12分
考点:本题主要考查等比数列的定义及通项公式,前n项求和公式,分组求和的方法,韦达定理。
点评: 综合题,从已知得到 ,
,  ,并对
,并对 进行改造是关键。
进行改造是关键。

练习册系列答案
相关题目
 =(cos
=(cos +sin
+sin =(cos
=(cos ,且f(x1)=f(x2)=1,求x1+x2的值.
,且f(x1)=f(x2)=1,求x1+x2的值.  、
、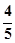 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。 (a
> 0,且a ≠ 1)的解集是{ x | x < 0 };
(a
> 0,且a ≠ 1)的解集是{ x | x < 0 }; 的定义域为R.如果
的定义域为R.如果 为真命题,
为真命题, 为假命题,
为假命题,