题目内容
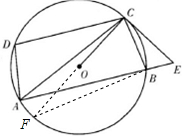
 如图,已知⊙O是四边形ABCD的外接圆,AD=BC,E是AB延长线上一点,且BE×DC=AD×BC.
如图,已知⊙O是四边形ABCD的外接圆,AD=BC,E是AB延长线上一点,且BE×DC=AD×BC.(Ⅰ)证明:AB∥CD;
(Ⅱ)求∠OCE的度数.
考点:与圆有关的比例线段,弦切角
专题:立体几何
分析:(I)由AD=BC,可得∴∠ACD=∠BAC,进而根据内错角相等,两直线平行得到AB∥CD;
(Ⅱ)根据圆内接四边形性质,可得∠ADC=∠EBC,由BE×DC=AD×BC得:
=
,进而可得△EBC∽△ADC,则∠BAC=∠ECB,延长CO交⊙O于F,连接BF,由∠FBC=90°,可得:∠OCE=∠ECB+∠BCF=∠BFC+∠BCF=90°.
(Ⅱ)根据圆内接四边形性质,可得∠ADC=∠EBC,由BE×DC=AD×BC得:
| BE |
| AD |
| BC |
| DC |
解答:
证明:(I)∵A,B,C,D四点共圆,且AD=BC,
∴∠ACD=∠BAC,
∴AB∥CD;
解:(Ⅱ)∵A,B,C,D四点共圆,
∴∠ADC=∠EBC,
∵BE×DC=AD×BC,即
=
,
∴△EBC∽△ADC,
∴∠BAC=∠ECB,
延长CO交⊙O于F,连接BF,
则∠FBC=90°,
∴∠BFC=∠BAC=∠ECB,
∴∠OCE=∠ECB+∠BCF=∠BFC+∠BCF=90°.
∴∠ACD=∠BAC,
∴AB∥CD;

解:(Ⅱ)∵A,B,C,D四点共圆,
∴∠ADC=∠EBC,
∵BE×DC=AD×BC,即
| BE |
| AD |
| BC |
| DC |
∴△EBC∽△ADC,
∴∠BAC=∠ECB,
延长CO交⊙O于F,连接BF,
则∠FBC=90°,
∴∠BFC=∠BAC=∠ECB,
∴∠OCE=∠ECB+∠BCF=∠BFC+∠BCF=90°.
点评:本题考查的知识点是也圆相关的比例线段,圆心角定理,圆周角定理,圆内接四边形性质,相似三角形的判断与性质,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知三棱锥P-ABC的所有顶点都在球O的球面上,AB=5,AC=3,BC=4,PB为球O的直径,PB=10,则这个三棱锥的体积为( )
A、30
| ||
B、15
| ||
C、10
| ||
D、5
|