题目内容
5.△ABC中,已知点A(-2,4),∠B的平分线BE所在直线方程式x-5y+9=0,且边BC的中点坐标为(0,0.5)(1)求△ABC的面积
(2)若点P是△ABC的外接圆上的动点,求$\frac{2y+3}{2x+3}$的取值范围.
分析 (1)根据BC边的中点D关于∠B平分线的对称点F在直线AB上,求出AB的直线方程,从而求出B、C点的坐标,再由点C到直线AB的距离d以及|AB|的长,求出△ABC的面积S;
(2)由|AB|、|BC|与|AC|的长,得出△ABC是直角三角形,从而求出△ABC的外接圆方程,把$\frac{2y+3}{2x+3}$看作圆M上的点P与定点Q(-$\frac{3}{2}$,$\frac{3}{2}$)连线的斜率,利用数形结合求出它的取值范围.
解答 解:(1)根据题意,设BC边的中点D关于∠B平分线的对称点为F(a,b),
则kDF=-$\frac{1}{{k}_{BE}}$,即$\frac{b-0.5}{a}$=-5①,
又DF的中点($\frac{a}{2}$,$\frac{b+0.5}{2}$)在直线x-5y+9=0上,
∴$\frac{a}{2}$-$\frac{5(b+0.5)}{2}$+9=0②,
由①、②组成方程组,解得a=-0.5,b=3;
∴点P(-0.5,3);
∴直线AB的方程为$\frac{x+2}{-0.5+2}$=$\frac{y-4}{3-4}$,
化简得2x+3y=8,
再由$\left\{\begin{array}{l}{2x+3y=8}\\{x-5y+9=0}\end{array}\right.$,
解得x=1,y=2,
∴点B(1,2);
又边BC的中点坐标为(0,0.5),
∴点C(-1,-1);
∴点C到直线AB的距离为d=$\frac{|2×(-1)+3×(-1)-8|}{\sqrt{{2}^{2}{+3}^{2}}}$=$\sqrt{13}$,
又|AB|=$\sqrt{{(1+2)}^{2}{+(2-4)}^{2}}$=$\sqrt{13}$,
∴△ABC的面积为S=$\frac{1}{2}$|AB|•d=$\frac{1}{2}$×$\sqrt{13}$×$\sqrt{13}$=$\frac{13}{2}$;
(2)△ABC中,|AB|=$\sqrt{13}$,|BC|=$\sqrt{13}$,|AC|=$\sqrt{26}$,
∴△ABC是直角三角形;
∴斜边AC的中点为M(-$\frac{3}{2}$,$\frac{3}{2}$),
∴△ABC的外接圆方程为${(x+\frac{3}{2})}^{2}$+${(y-\frac{3}{2})}^{2}$=$\frac{13}{2}$;
又$\frac{2y+3}{2x+3}$=$\frac{y-(-\frac{3}{2})}{x-(-\frac{3}{2})}$,
∴上式可以看作圆M上的点P(x,y)与定点Q(-$\frac{3}{2}$,$\frac{3}{2}$)连线的斜率,
设PQ的斜率为k,则PQ的直线方程为y+$\frac{3}{2}$=k(x+$\frac{3}{2}$),
即kx-y+$\frac{3}{2}$k-$\frac{3}{2}$=0,
则点M(-$\frac{3}{2}$,$\frac{3}{2}$)到PQ的距离为d=r;
即$\frac{|-\frac{3}{2}k-\frac{3}{2}+\frac{3}{2}k-\frac{3}{2}|}{\sqrt{1{+k}^{2}}}$=$\frac{\sqrt{26}}{2}$,
解得k=±$\frac{\sqrt{65}}{13}$;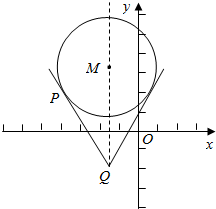
由图形得,k的取值范围是{k|k≤-$\frac{\sqrt{65}}{13}$,或k≥$\frac{\sqrt{65}}{13}$}.
点评 本题考查了直线与圆的应用问题,考查了点关于直线对称的应用问题,也考查了三角形的外接圆方程的应用问题,是综合性题目.

| A. | 各个面都是三角形的几何体是三棱锥 | |
| B. | 以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥 | |
| C. | 圆锥的顶点与底面圆周上的任意一点的连线都是母线 | |
| D. | 棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是六棱锥 |
| A. | a?平面α,b?平面α,a与b不平行 | |
| B. | a?平面α,b?平面α,a与b不相交 | |
| C. | a∥直线c,b∩c=A,b与a不相交 | |
| D. | a?平面α,b?平面β,α∩β=l,a与b无公共点 |
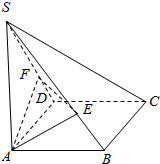 如图所示,四边形ABCD为正方形,SA垂直于四边形ABCD所在的平面,过点A分别作AE⊥SB,AF⊥SD,垂足分别为点E和点F,求证:EF⊥SC.
如图所示,四边形ABCD为正方形,SA垂直于四边形ABCD所在的平面,过点A分别作AE⊥SB,AF⊥SD,垂足分别为点E和点F,求证:EF⊥SC.