题目内容
设f(x)＝ax3－
(a＋2)x2＋6x－3，x∈R，a是常数，且a＞0
(Ⅰ)求f(x)的单调递增区间；
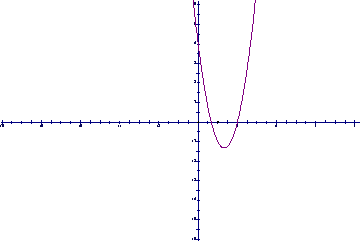
(Ⅱ)若f(x)在x＝1时取得极大值，且直线y＝－1与函数f(x)的图象有三个交点，求实数a的取值范围．
答案：
解析：
解析：
|
解：(Ⅰ)∵ ∴ ①当 ②当 ③当 综上所述，当 当 当 (Ⅱ)∵ ∴ |
，
时，有
，由
得
或
，∴
的单调递增区间是
和
时，
恒成立，且只有
，∴
时，有
，由
或
，∴
和
时取得极大值，由(Ⅰ)知，
，
，∵直线
与函数f(x)的图象有三个交点，
，解得
(12分)
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
(x)的图象经过点(
，0)，(2，0)，如图所示．
(x)的最小值为－12．