题目内容
已知数列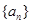 满足
满足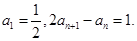
(1)求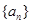 的通项公式;
的通项公式;
(2)证明: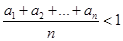 .
.
(1) ;(2)见解析.
;(2)见解析.
解析试题分析:(1)根据所给的 将
将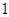 拆为
拆为 ,化简得到关系
,化简得到关系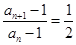 ,构造数列
,构造数列 ,证明此数列是以
,证明此数列是以 为首项,
为首项, 为公比的等比数列,求得
为公比的等比数列,求得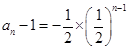 ,即得
,即得 ;(2)根据所求的通项公式以及等比数列的前
;(2)根据所求的通项公式以及等比数列的前 项和公式求得
项和公式求得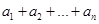
 ,那么就有
,那么就有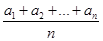
 ,由
,由 是整数以及指数函数的性质可知
是整数以及指数函数的性质可知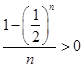 ,所以
,所以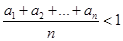 得证.
得证.
试题解析:(1)由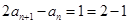 可得,
可得,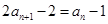 ,即
,即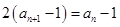 2分
2分
∴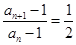 , 4分
, 4分
由 得,
得, , . 5分
, . 5分
∴数列 是以
是以 为首项,
为首项, 为公比的等比数列, 6分
为公比的等比数列, 6分
∴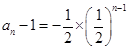 ,∴
,∴ . .7分
. .7分
(2)证明:∵ .9分
.9分 ..10分
..10分 . 11分
. 11分
∴ , .12分
, .12分
∵ 是正整数,∴
是正整数,∴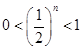 ,
, , ..13分
, ..13分
∴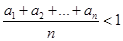 . . 14分
. . 14分
考点:1.等比数列的定义;2.等比数列的前 项和公式;3.指数函数的性质
项和公式;3.指数函数的性质

练习册系列答案
相关题目
 an=1.
an=1. ,数列
,数列 的前n项和为Tn,证明:Tn<
的前n项和为Tn,证明:Tn< .
. 为递增数列,且
为递增数列,且 ,
, .(Ⅰ)求
.(Ⅰ)求 ;
; ,不等式
,不等式 的解集为
的解集为 ,求所有
,求所有 的和.
的和. 中,
中,
 是等比数列,并求
是等比数列,并求 ;
; 满足
满足 ,数列
,数列 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围。
的取值范围。 满足:①
满足:①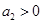 ;②对于任意正整数
;②对于任意正整数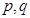 都有
都有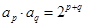 成立.
成立.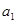 的值;
的值;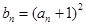 ,求数列
,求数列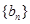 的前
的前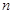 项和.
项和. }的前n项和为
}的前n项和为 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数 且
且 均为常数)的图像上.
均为常数)的图像上.  求数列
求数列 的前
的前 项和
项和 .
. 的前
的前 项和是
项和是 ,且
,且 .
. ,求适合方程
,求适合方程 的正整数
的正整数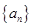 的前
的前 项和为
项和为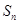 ,点
,点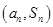 在直线
在直线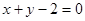 上,
上,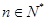 .(1)证明数列
.(1)证明数列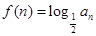 ,记
,记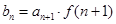 ,求数列
,求数列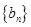 的前
的前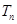 .
.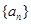 的前
的前 项和为
项和为 ,
, ,且
,且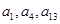 成等比数列.
成等比数列.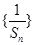 的前
的前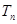 的表达式。
的表达式。