题目内容
已知椭圆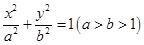 内有圆
内有圆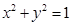 ,如果圆的切线与椭圆交A、B两点,且满足
,如果圆的切线与椭圆交A、B两点,且满足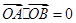 (其中
(其中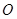 为坐标原点).
为坐标原点).
(1)求证: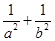 为定值;
为定值;
(2)若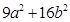 达到最小值,求此时的椭圆方程;
达到最小值,求此时的椭圆方程;
(3)在满足条件(2)的椭圆上是否存在点P,使得从P向圆所引的两条切线互相垂直,如果存在,求出点的坐标,如果不存在,说明理由.
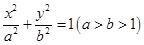 内有圆
内有圆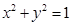 ,如果圆的切线与椭圆交A、B两点,且满足
,如果圆的切线与椭圆交A、B两点,且满足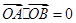 (其中
(其中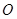 为坐标原点).
为坐标原点).(1)求证:
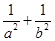 为定值;
为定值;(2)若
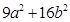 达到最小值,求此时的椭圆方程;
达到最小值,求此时的椭圆方程;(3)在满足条件(2)的椭圆上是否存在点P,使得从P向圆所引的两条切线互相垂直,如果存在,求出点的坐标,如果不存在,说明理由.
解:(1)方法1:设圆的切线的切点坐标为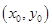 ,则切线的方程为
,则切线的方程为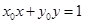 ,与椭圆方程联立消去
,与椭圆方程联立消去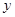 得:
得: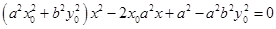 .
.
设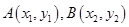 ,因
,因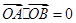 ,所以
,所以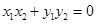 ,又
,又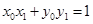 ,
,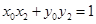 ,所以
,所以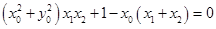 .(*)
.(*)
将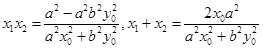 代入(*)得
代入(*)得
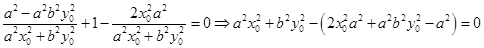 ,
,
因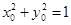 ,因此
,因此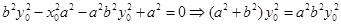 ,所以
,所以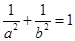 (定值).
(定值).
方法2:设切线的方程为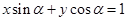 ,则有
,则有
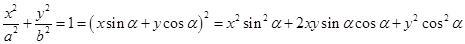 ,
,
所以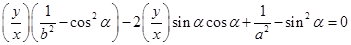 .
.
因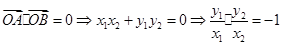 ,所以
,所以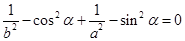 ,即
,即
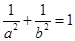 (定值).
(定值).
(2)因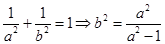 ,
,
所以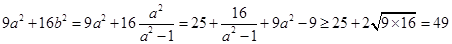 .
.
当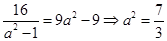 时取到最小值,此时椭圆的方程为
时取到最小值,此时椭圆的方程为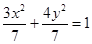 .
.
(3)如果存在满足条件的点P,则向圆引两条切线,切点分别为M、N,连结OM、ON,则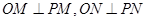 ,如果
,如果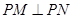 ,则四边形OMPN为正方形,所以
,则四边形OMPN为正方形,所以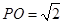 ,因为椭圆
,因为椭圆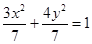 上到中心最近的点为短轴的端点,距离为
上到中心最近的点为短轴的端点,距离为 ,故存在四个点满足条件,其坐标为
,故存在四个点满足条件,其坐标为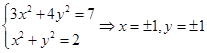 ,即
,即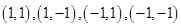 .
.
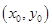 ,则切线的方程为
,则切线的方程为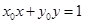 ,与椭圆方程联立消去
,与椭圆方程联立消去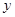 得:
得: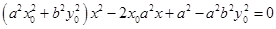 .
.设
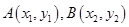 ,因
,因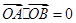 ,所以
,所以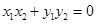 ,又
,又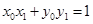 ,
,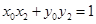 ,所以
,所以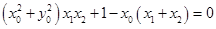 .(*)
.(*)将
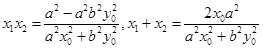 代入(*)得
代入(*)得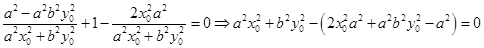 ,
,因
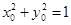 ,因此
,因此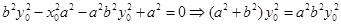 ,所以
,所以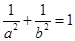 (定值).
(定值).方法2:设切线的方程为
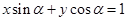 ,则有
,则有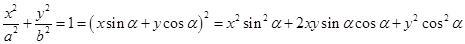 ,
,所以
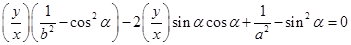 .
.因
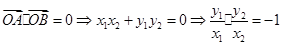 ,所以
,所以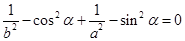 ,即
,即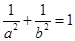 (定值).
(定值).(2)因
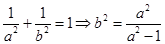 ,
,所以
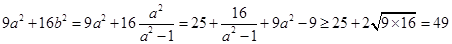 .
.当
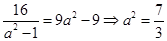 时取到最小值,此时椭圆的方程为
时取到最小值,此时椭圆的方程为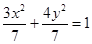 .
.(3)如果存在满足条件的点P,则向圆引两条切线,切点分别为M、N,连结OM、ON,则
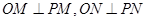 ,如果
,如果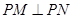 ,则四边形OMPN为正方形,所以
,则四边形OMPN为正方形,所以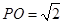 ,因为椭圆
,因为椭圆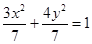 上到中心最近的点为短轴的端点,距离为
上到中心最近的点为短轴的端点,距离为 ,故存在四个点满足条件,其坐标为
,故存在四个点满足条件,其坐标为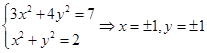 ,即
,即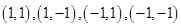 .
.略

练习册系列答案
相关题目
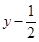 )2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.
)2=r2(r>0)有一个公共点,且在A处两曲线的切线为同一直线l.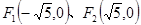 ,直线PF1和PF2相交于点P,且它们的斜率之积为定值
,直线PF1和PF2相交于点P,且它们的斜率之积为定值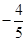 ;
;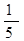 ),N为抛物线C2:
),N为抛物线C2: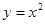 上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求
上的一动点,过点N作抛物线C2的切线交曲线C1于P、Q两点,求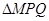 面积的最大值.
面积的最大值. ABC内(含边界)一动点,且到三个侧面PAB,PBC,PCA的距离成等差数列,则点M的轨迹是( )
ABC内(含边界)一动点,且到三个侧面PAB,PBC,PCA的距离成等差数列,则点M的轨迹是( ) O方程为
O方程为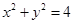 ,点P在圆上,点D在x轴上,点M在DP延长线上,
,点P在圆上,点D在x轴上,点M在DP延长线上,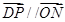 .且
.且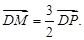
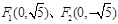 ,若过F1的直线交(I)中曲线C于A、B两点,求
,若过F1的直线交(I)中曲线C于A、B两点,求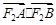 的取值范围.
的取值范围.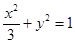 ,过坐标原点O作两条互相垂直的射线,与椭圆分别交于A,B两点.
,过坐标原点O作两条互相垂直的射线,与椭圆分别交于A,B两点.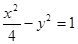 的渐近线与圆
的渐近线与圆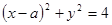 相切,则
相切,则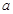 = .
= .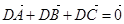 ;②|
;②|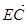 |=
|=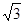 |
|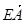 |=
|=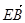 |③
|③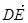 与
与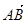 共线.
共线.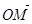 ·
·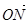 =0,求直线l的方程.
=0,求直线l的方程.