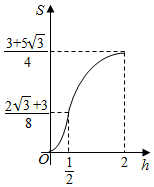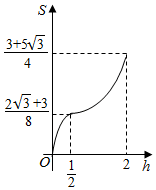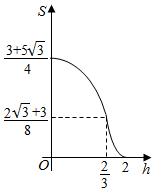题目内容
13．函数y=-$\frac{1}{2}$x2+x+m的最大值是3m-$\frac{1}{2}$，则m的值是（ ）| A． | 4 | B． | 2 | C． | 1 | D． | $\frac{1}{2}$ |
分析 通过配方求出y的最大值，得到关于m的方程，解出即可．
解答 解：函数y=-$\frac{1}{2}$x2+x+m=-$\frac{1}{2}$（x-1）2+$\frac{1}{2}$+m的最大值是3m-$\frac{1}{2}$，
则$\frac{1}{2}$+m=3m-$\frac{1}{2}$，解得：m=$\frac{1}{2}$，
故选：D．
点评 本题考查了求函数的最大值问题，考查二次函数的性质，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
4．设函数f（x）=$\left\{\begin{array}{l}cosπx，x＞0\\ f（x+1）-1，x≤0\end{array}$，则f（-$\frac{4}{3}$）的值为（ ）
| A． | $-\frac{3}{2}$ | B． | $\frac{{\sqrt{3}}}{2}-2$ | C． | $-\frac{{\sqrt{3}}}{2}-2$ | D． | $-\frac{5}{2}$ |
1．
已知三棱锥的三视图如图所示，其中侧视图是边长为$\sqrt{3}$的正三角形，则该几何体的外接球的体积为（ ）
已知三棱锥的三视图如图所示，其中侧视图是边长为$\sqrt{3}$的正三角形，则该几何体的外接球的体积为（ ）| A． | $\frac{16π}{3}$ | B． | $\frac{32}{3}π$ | C． | 4$\sqrt{3}$π | D． | 16π |
8．
某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况，随机对50人做了问卷调查，得如下频数分布表：
（1）做出这些数据的频率分布直方图并估计次境外旅游线路游客的人均购物的消费平均值；
（2）在调查问卷中有一项是“您会资助失学儿童的金额？”，调查情况如表，请补全如表，并说明是否有95%以上的把握认为资助数额多于或少于500元和自身购物是否到4000元有关？
附：临界值表参考公式：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
某旅游为了解2015年国庆节期间参加某境外旅游线路的游客的人均购物消费情况，随机对50人做了问卷调查，得如下频数分布表：| 人均购物消费情况 | [0，2000] | （2000，4000] | （4000，6000] | （6000，8000] | （8000，10000] |
| 额数 | 15 | 20 | 9 | 3 | 3 |
（2）在调查问卷中有一项是“您会资助失学儿童的金额？”，调查情况如表，请补全如表，并说明是否有95%以上的把握认为资助数额多于或少于500元和自身购物是否到4000元有关？
| 人均购物消费不超过4000元 | 人均购物消费超过4000元 | 合计 | |
| 资助超过500元 | 30 | ||
| 资助不超过500元 | 6 | ||
| 合计 |
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
18．
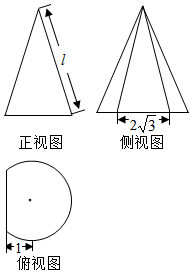如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图，其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$，则圆锥的母线长为（ ）
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图，其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$，则圆锥的母线长为（ ）| A． | $2\sqrt{2}$ | B． | $2\sqrt{3}$ | C． | 4 | D． | $\sqrt{2}+\sqrt{3}$ |
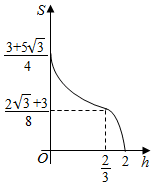
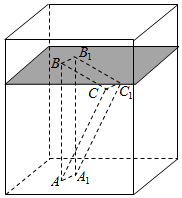已知三棱柱ABC-A1B1C1，侧棱BB1⊥平面ABC，AB=2，AC=$\sqrt{3}$，AA1=$\frac{1}{4}$，AC⊥BC，将其放入一个水平放置的水槽中，使AA1在水槽底面内，平面ABB1A1与水槽底面垂直，且水面恰好经过棱BB1，现水槽底面出现一个洞，水位下降，则在水位下降过程中，几何体露出水面部分的面积S关于水位下降的高度h的图象大致为（ ）
