题目内容
在平面直角坐标系 中,已知曲线
中,已知曲线 :
:  ,在极坐标系(与平面直角坐标系
,在极坐标系(与平面直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的极坐标方程为
的极坐标方程为 .
.
(1)将曲线 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 倍、
倍、 倍后得到曲线
倍后得到曲线 ,试写出直线
,试写出直线 的直角坐标方程和曲线
的直角坐标方程和曲线 的参数方程;
的参数方程;
(2)在曲线 上求一点
上求一点 ,使点
,使点 到直线
到直线 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.
 中,已知曲线
中,已知曲线 :
:  ,在极坐标系(与平面直角坐标系
,在极坐标系(与平面直角坐标系 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的极坐标方程为
的极坐标方程为 .
.(1)将曲线
 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 倍、
倍、 倍后得到曲线
倍后得到曲线 ,试写出直线
,试写出直线 的直角坐标方程和曲线
的直角坐标方程和曲线 的参数方程;
的参数方程;(2)在曲线
 上求一点
上求一点 ,使点
,使点 到直线
到直线 的距离最大,并求出此最大值.
的距离最大,并求出此最大值.(1) ,
, ;(2)当
;(2)当 时
时 .
.
 ,
, ;(2)当
;(2)当 时
时 .
.试题分析:
解题思路:(1)利用直线与椭圆的参数方程与普通方程的互化公式求解即可;(II)利用点到直线的距离公式转化从三角函数求最值即可求解.
规律总结:参数方程与普通方程之间的互化,有公式可用,较简单;往往借助参数方程研究直线与椭圆的位置关系或求最值.
试题解析:(1)由题意知,直线
 的直角坐标方程为
的直角坐标方程为 ,
, 由题意知曲线
 的直角坐标方程为
的直角坐标方程为 ,
, ∴曲线
 的参数方程为
的参数方程为 (
( 为参数).
为参数). (2)设
 ,则点
,则点 到直线
到直线 的距离
的距离 ,
, 当
 时,即点
时,即点 的坐标为
的坐标为 时,点
时,点 到直线
到直线 的距离最大,
的距离最大,此时
 .
.
练习册系列答案
相关题目
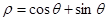 和直线
和直线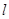 :
: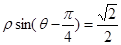 .
.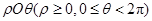 中,点
中,点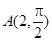 关于直线
关于直线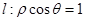 的对称点的极坐标为 .
的对称点的极坐标为 .  (t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为_______________.
(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为_______________. 为极点的极坐标系中,圆
为极点的极坐标系中,圆 和直线
和直线 相交于
相交于 两点.若
两点.若 是等边三角形,则
是等边三角形,则 的值为___________.
的值为___________. 成反比,动点P的轨迹经过点(2,0).
成反比,动点P的轨迹经过点(2,0).