题目内容
10.根据下列条件,求抛物线的标准方程.(1)焦点坐标为(-2,0);
(2)准线方程为y=-1;
(3)过点(1,2).
分析 直接利用抛物线的性质结合已知求得(1)(2)的标准方程;设出抛物线方程y2=2px(p>0)或x2=2py(p>0),把点的坐标代入求得p,则(3)的方程可求.
解答 解:(1)∵抛物线的焦点坐标为(-2,0),∴$\frac{p}{2}=2$,则p=4,故抛物线方程为y2=-8x;
(2)∵抛物线准线方程为y=-1,∴$\frac{p}{2}=1$,则p=2,故抛物线方程为x2=4y;
(3)∵抛物线过点(1,2),∴可设抛物线方程为y2=2px(p>0)或x2=2py(p>0),
把点(1,2)代入y2=2px,得p=2,故抛物线方程为y2=4x;
代入x2=2py,得p=$\frac{1}{4}$,故抛物线方程为${x}^{2}=\frac{1}{2}y$.
∴所求抛物线方程为y2=4x或${x}^{2}=\frac{1}{2}y$.
点评 本题考查抛物线的标准方程,考查了抛物线的简单性质,是基础题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
1.已知数列{an}的通项公式an=2015sin$\frac{nπ}{2}$,则a1+a2+…+a2015=( )
| A. | -2015 | B. | 2015 | C. | 0 | D. | 2014 |
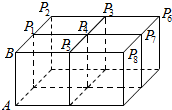 如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )
如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )