题目内容
10.已知$\overrightarrow a$=(1,1,0),$\overrightarrow b$=(-1,0,2),且$k\overrightarrow a+\overrightarrow b$与$\overrightarrow a-\overrightarrow b$互相垂直,则k的值为2.分析 根据空间向量的坐标运算与数量积的坐标表示,列出方程解方程即可.
解答 解:∵$\overrightarrow a$=(1,1,0),$\overrightarrow b$=(-1,0,2),
∴$k\overrightarrow a+\overrightarrow b$=(k-1,k,2),
$\overrightarrow a-\overrightarrow b$=(2,1,-2),
又($k\overrightarrow a+\overrightarrow b$)⊥($\overrightarrow a-\overrightarrow b$),
∴2(k-1)+k-4=0,
解得k=2.
故答案为:2.
点评 本题考查了空间向量的坐标运算与数量积的坐标表示问题,是基础题目.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
1.已知平面向量$\overrightarrow a$,$\overrightarrow b$的夹角为$\frac{2π}{3}$,且$|{\overrightarrow a}$|=2,$\overrightarrow a•\overrightarrow b=-1$,则$|{\overrightarrow b}$|=( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
18.下列函数中,最小正周期为$\frac{π}{2}$的是( )
| A. | y=sinx | B. | y=cos4x | C. | y=tan$\frac{x}{2}$ | D. | y=sinx+cosx |
5.函数f(x)=$\frac{ln(x-1)}{{\sqrt{2-x}}}$的定义域为( )
| A. | (1,2) | B. | (1,2] | C. | (-∞,2] | D. | (1,+∞) |
15.$\frac{10i}{1-2i}$ 复数( )
| A. | 4-2i | B. | -4+2i | C. | 2+4i | D. | 2-4i |
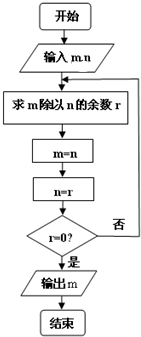 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“辗转相除法”,执行该程序框图,若输入的m,n分别为112,91,则输出的m为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“辗转相除法”,执行该程序框图,若输入的m,n分别为112,91,则输出的m为( )