题目内容
在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是:“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”.

试题分析:建立从平面图形到空间图形的类比,于是作出猜想
 ,证明如下:由于三棱锥
,证明如下:由于三棱锥 的三个侧面
的三个侧面 两两相互垂直,所以三条侧棱
两两相互垂直,所以三条侧棱 两两垂直,可证明
两两垂直,可证明 面
面 ,则
,则 ,在
,在 中,过点
中,过点 作
作 ,垂足为
,垂足为 ,连接
,连接 ,∵
,∵ ,
, 面
面 ,∴
,∴ ,
, =
= =
= =
= =
= =
= =
= .
.

练习册系列答案
相关题目
 ,O为AB的中点.
,O为AB的中点.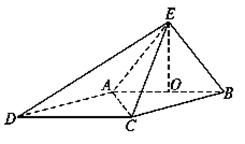


 ,求证:平面ADE⊥平面PBC
,求证:平面ADE⊥平面PBC 中,底面
中,底面 是矩形,
是矩形, 平面
平面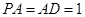 ,
,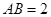 ,
,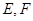 分别是
分别是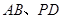 的中点.
的中点.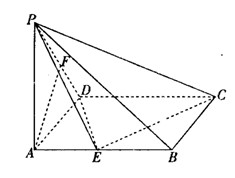
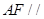 平面
平面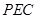 ;
; 的余弦值.
的余弦值. 所在的平面与正方形
所在的平面与正方形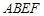 所在的平面相互垂直,
所在的平面相互垂直,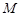 、
、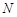 分别是
分别是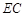 、
、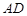 的中点.
的中点.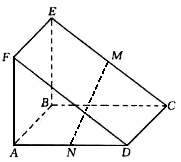
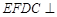 面
面 ;
;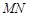 与平面
与平面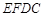 所成的角正弦值.
所成的角正弦值.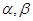 是不重合的平面,下列命题正确的是( ):
是不重合的平面,下列命题正确的是( ):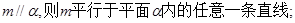

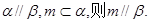

 、
、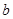 与平面
与平面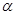 ,下列命题正确的是( )
,下列命题正确的是( )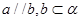 ,则
,则
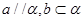 ,则
,则
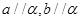 ,则
,则 则
则 ,
,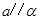 ,
,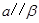 ,则
,则 与
与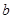 的位置关系是_______.
的位置关系是_______.